1、机器学习概述

1-1、机器学习定义

Two definitions of Machine Learning are offered.
Machine Learning is the field of study that gives computers the ability to learn without being explicitly programmed.
A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.

1-2、机器学习分类

机器学习问题可以大致被分为监督学习（supervised learning）和非监督学习（unsupervised learning），其它还有强化学习（reinforcement learning）和推荐系统（recommender systems）。

1-3、Supervised Learning 监督学习

We give the algorithm a dataset in which the ‘right answers’ are given, the algorithm is to produce more of these right answers.
给一个算法，需要部分数据集已经有正确答案，根据算法分析已知数据集从而得到更多数据的“正确答案”。
监督学习又可以被分为回归问题和分类问题两类:

1-3-1、Regression Problem 回归问题

predict continuous valued output 预测一个连续值输出
典型例子:房价预测 Housing Price Prediction

1-3-2、Classification Problem 分类问题

predict discrete valued output 预测一个离散值输出
典型例子:判断良性恶性肿瘤
在分类问题中，有时会有超过两个的输出值（比如无癌症、胃癌、肺癌、肝癌），但仍然是可数的，离散的。
在分类问题中，可能有不止一个的特征和属性，但是算法能够处理无穷多个特征，利用一种叫Support Vector Machine 支持向量机的算法（一个简洁的数学方法，能够让电脑处理无限多的特征）。

1-4、Unsupervised Learning 非监督学习

We can derive this structure by clustering the data based on relationships among the variables in the data.
非监督学习是一种学习机制，你给算法大量的数据，要求它找出数据中蕴含的类型结构。
在非监督学习中，数据没有属性或者标签的概念，所有的数据都是一样的，没有任何区别（而你的目标就是找出区别，并且把数据分类）。
With unsupervised learning there is no feedback based on the prediction results.
非监督学习主要可以分为聚类算法问题和非聚类算法问题两种：

1-4-1、Clustering Algorithm 聚类算法

将一个数据集分成几个聚类，这就是聚类算法。
典型例子是google新闻，它把成千上万的新闻聚集起来，按照每个新闻的内容分成一个一个的专题。

1-4-2、Cocktail Party Algorithm 鸡尾酒会算法（Non-clustering Algorithm 非聚类算法）

鸡尾酒宴问题
有一个宴会，有一屋子的人，大家都坐在一起，而且在同时说话，有许多声音混杂在一起，因为每个人都是在同一时间说话的，在这种情况下你很难听清楚你面前的人说的话。因此，比如有这样一个场景，宴会上只有两个人，同时说话， 有两个麦克风，把它们放在房间里，然后因为这两个麦克风距离这两个人的距离不同，每个麦克风都记录下了来自两个人的声音的不同组合。A的声音在第一个麦克风里的声音会响一点，B的声音在第二个麦克风里会比较响一点，因为两个麦克风的位置相对于两个说话者的位置是不同的。但每个麦克风都会录到来自两个说话者的重叠部分的声音。
Cocktail Party Algorithm
Separate out these two audio sources that were being added or being summed together to from other recordings.
鸡尾酒会算法：找出其中蕴含的分类，算法还会分离出两个被叠加到一起的音频源。
代码：$[W,s,v]=svd((repmat(sum(x.x,1),size(x,1),1).x)*x’);$

2、Linear Regression with One Variable 单变量线性回归

Notation 部分使用符号

$m$ = Number of training examples 训练样本的数目
$x’s$ = “input” variable / features 输入变量/特征量
$y’s$ = “output” variable / “target” variable 输出变量/目标变量
$(x,y)$ = one training example 某一个训练样本（泛指）
$(x^{(i)},y^{(i)})$ ith training example 第i个训练样本（特指）
Training Set: a list of $m$ training examples $(x^{(i)} , y^{(i)} ); i =1, . . . , m$

2-1、Model Representation 模型表示

我们将训练集数据交给学习算法，将会得到一个函数，通常用h来表示,h则代表hypothesis 假设。对于函数h，输入变量x’s,得到输出y’s。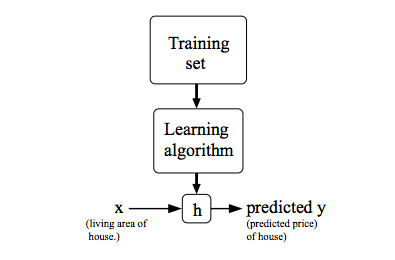

2-2、Linear Regression with One Variable Model (Univariate Linear Regression)单变量线性回归模型

我们以这个公式来表示函数h：$h_\theta(x)=\theta_0+\theta_1x$
我们要预测一个关于x的线性函数，当然非线性函数也是可能的。

2-3、Cost Function 代价函数

$\theta_i’s$ = the parameters of the model 模型参数
我们要选择能使$h(x)$，也就是输入$x$时我们预测的值最接近该样本对应的y值的参数$\theta_0,\theta_1$。
在线性回归中，我们要解决的是一个最小化问题。
$$\displaystyle\min_{\theta_0,\theta_1}\dfrac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2$$
这是线性回归的整体目标函数，但是为了方便，我们定义一个代价函数。
$$\begin{cases}
J(\theta_0,\theta_1)=\dfrac{1}{2m}\displaystyle\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2\\
\min_{\theta_0,\theta_1}J(\theta_0,\theta_1)
\end{cases}$$
我们要做的就是关于$\theta_0$和$\theta_1$，对函数$J(\theta_0,\theta_1)$求最小值，这个函数也被称为Squared Error Function 平方误差函数。
平方误差代价函数对于大多数问题，特别是回归问题，都是一个合理的选择，还有其他的代价函数也能很好地发挥作用，但是平方误差代价函数可能是解决回归问题最常用的手段了。

2-3-1、直观理解一

为了更好理解假设函数与代价函数，不妨假设$\theta_0=0$，即$h_\theta(x)=\theta_1x$，此时假设函数只有一个模型参数$\theta_1$。
对应的代价函数也变成了$J(\theta_1)=\dfrac{1}{2m}\displaystyle\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2=\dfrac{1}{2m}\sum_{i=1}^m(\theta_1x^{(i)}-y^{(i)})^2$，也就是说现在代价函数只有一个自变量，从图形上来理解就是我们选择的假设函数会经过（0，0）点。

2-3-2、直观理解二

一般的，我们考察$J(\theta_0,\theta_1)$函数的图形，我们会发现函数图形（三维）是呈现一个倒置伞状的（实际上这取决于训练样本）。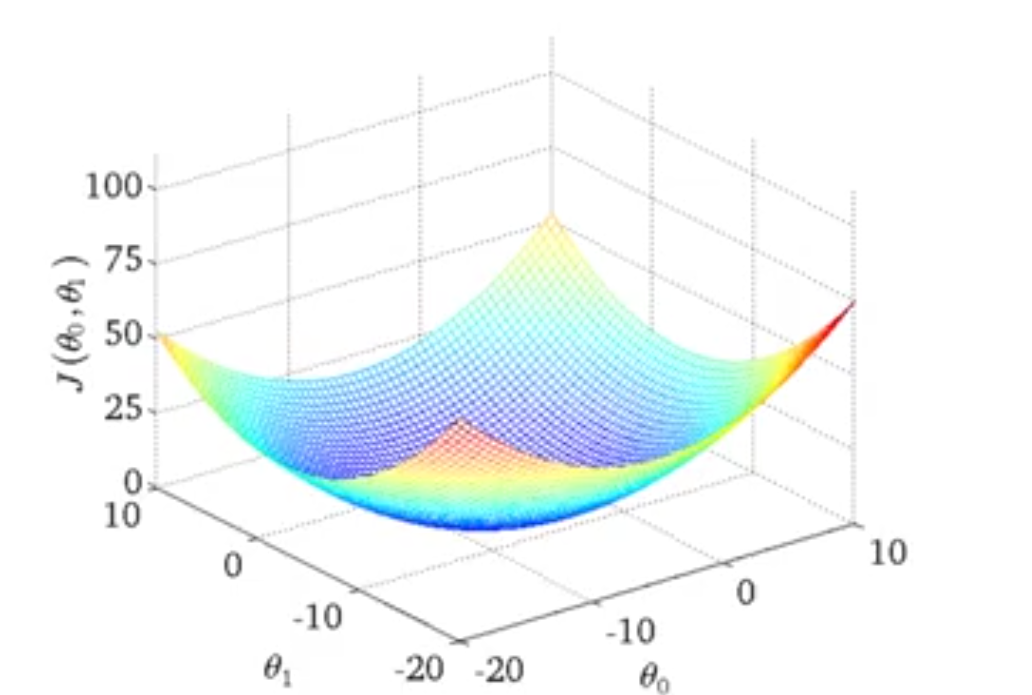

还有一种图形表现是contour plot 轮廓图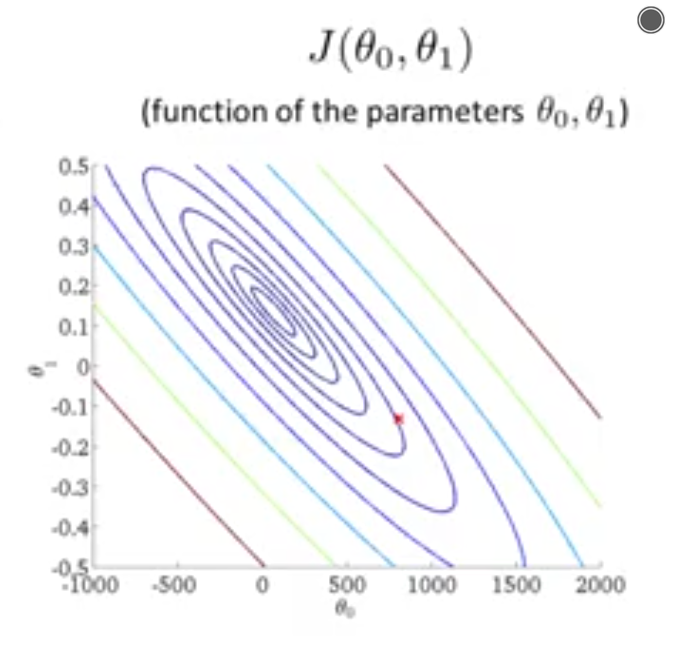

两个轴分别表示两个模型参数，图表里面包含一圈一圈的椭圆形，每一个圈就表示函数值相同的所有点的集合。理解的话，想象刚才的伞形图形从屏幕中冒出来，在同一时刻伞形图形与屏幕相交的边就是这些一圈一圈的椭圆形，在椭圆上的每个点函数值相同。（可以类比高中地理的等势图）
对于多维度、多参数的代价函数，我们很难实现它的图形化，但我们可以编写程序来自动地找到使代价函数最小的参数组合。

2-4、Gradient Descent 梯度下降算法

梯度下降算法可以将代价函数$J$最小化，它是很常用的算法，它不仅被用在线性回归上。
假设有某个代价函数$J(\theta_0,\theta_1)$，想要最小化这个函数。这个函数可以是一个线性回归的代价函数，也可以是一些其他函数。当然，梯度下降算法不止使用于两个参数的情况，可以使用于多个参数的情况，梯度下降算法可以解决更加一般的问题。
但是，需要注意的是，使用梯度下降算法也必须满足一定的条件。需要被最小化的函数一定是一个凸函数（也就是呈一个伞状，即没有区部最优值），如果不满足这个条件的话，只能使用模拟退火算法。

2-4-1、Outline 构想

1、Start with some $\theta_0,\theta_1$：对$\theta_0$和$\theta_1$进行初步的猜测（通常选择将$\theta_0$和$\theta_1$都设为0）。
2、Keep changing $\theta_0,\theta_1$ to reduce $J(\theta_0,\theta_1)$ until we hopefully end up at a minimum 不停地改变$\theta_0$和$\theta_1$，试图通过这种改变使得$J(\theta_0,\theta_1)$变小，直到我们找到J的最小值。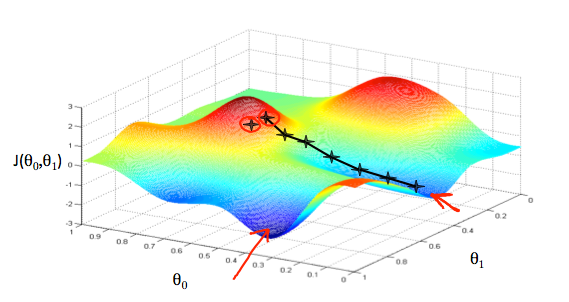

2-4-2、特点

起始点的位置略有不同，你就可能会得到一个不同的局部最优解，这是梯度下降算法的一大特点。

2-4-3、算法定义

$\text{repeat until convergence [}\\
　　　　\theta_j:={\theta}_j-\alpha\dfrac{\partial}{\partial{\theta}_j}J({\theta}_0,{\theta}_1)　　　(for:j=0　\text{and}　:j=1)\\
\text{]}$

2-4-4、说明

$:=$表示赋值运算符。
$=$ 表示相等断言，即声明$a$的值与$b$的值相同。
$\alpha$ 是一个常数，被称为learning rate 学习速率。在梯度下降算法中，它控制了我们下降时会迈出的步长。
在这个等式中，我们需要同时更新$\theta_0$和$\theta_1$，而不是两者单独更新。
Correct: Simlultaneous update
$temp0:=\theta_0-\alpha\dfrac{\partial}{\partial\theta_0}J(\theta_0,\theta_1)$
$temp1:=\theta_1-\alpha\dfrac{\partial}{\partial\theta_1}J(\theta_0,\theta_1)$
$\theta_0:=temp0$
$\theta_1:=temp1$

2-4-5、直观理解

根据导数的图形意义和公式的数学定义，可以看出$\theta$点是向局部最小点趋近的。
$\alpha$太小，收敛速度会很慢。
$\alpha$太大，那么梯度下降算法可能会越过最低点，甚至因无法收敛而导致发散。
当$\theta$点已经收敛于局部最小值，而局部最优点的导数将等于0，所以在梯度下降的过程中，模型参数将不会改变。
梯度下降算法能收敛到局部最小值，即便学习率$\alpha$是固定的。当$\theta$点接近局部最小值的时候，梯度下降算法会自动地采取更小的步伐（下山）。所以，我们不需要手动减小$\alpha$。

2-4、线性回归

将梯度下降和代价函数结合起来，得到具体的拟合直线的线性回归算法，并用梯度下降的方法来最小化平方误差代价函数。
那么，我们首先就需要弄清楚梯度下降算法中的偏导项：
$$\dfrac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)=\dfrac{\partial}{\partial\theta_j}\dfrac{1}{2m}\displaystyle\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2\\=\dfrac{\partial}{\partial\theta_j}\dfrac{1}{2m}\displaystyle\sum_{i=1}^m(\theta_0+\theta_1x^{(i)}-y^{(i)})^2$$
$$j=0:　　\dfrac{\partial}{\partial\theta_0}J(\theta_0,\theta_1)=\dfrac{1}{m}\displaystyle\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})$$
$$j=1:　\dfrac{\partial}{\partial\theta_1}J(\theta_0,\theta_1)=\dfrac{1}{m}\displaystyle\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x^{(i)}$$
下面写出$\theta_j$式子的偏导过程：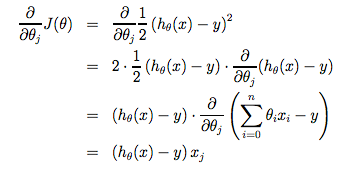

将得到的导数项代回式子，得到
$\text{repeat until convergence [}\\
　　　　{\theta}_0:={\theta}_0-\alpha\dfrac{1}{m}\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)}) \\
　　　　{\theta}_1:={\theta}_1-\alpha\dfrac{1}{m}\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)} \\
\text{]} \\
\text{update $\theta_0$ and $\theta_1$ simultaneously}$
对于线性回归模型，它的图形永远是呈现出倒置伞形的，即它的代价函数是一个凸函数，它只有一个全局最优解，所以适用梯度下降算法。

2-5、“Batch” Gradient Descent 批量梯度下降

“Batch”：Each step of gradient descent uses all the training examples. 在梯度下降的每一步中，我们都用到了所有的训练样本。
所以这里使用的梯度下降算法又叫批量梯度下降算法。
但是缺点也同样很明显，当训练集较为庞大时，运行梯度下降的时间将大大增加。

2-6、Normal Equations 正规方程

还有另一种求解代价函数最小值的数值解法，不需要梯度下降这种迭代算法。它可以在不需要多步梯度下降的情况下，也能解出代价函数的最小值。实际上，在数据量较大的情况下，梯度下降比正规方程要更适用一些。