1、Linear Algebra Review 线性代数复习
1-1、Matrices and Vectors 矩阵和向量
1-1-1、What are Matrices
$\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}$
Matrix: Rectangular array of numbers written between square brackets. 由数字组成的矩阵阵列
Demension of matrix: number of rows $\times$ number of columns 矩阵的维度写作矩阵的行数X列数
一般用$R^{a\times b}$表示行数为$a$、列数为$b$的所有矩阵集合。
1-1-2、Matrix Elements(entries of matrix) 矩阵元素
$A_{ij}$ = “ $i$,$j$ entry “ in the $i^{th}$ row,$j^{th}$ column.
1-1-3、What are Vectors
$\begin{bmatrix} 460 \\ 232 \\ 315 \\ 178 \end{bmatrix}$
Vector: An $n\times 1$ matrix. 一个向量是一种特殊的矩阵,向量只有一列。
Demension of vector: 向量的维度就是它的行数。
我们同样使用$R^a$表示维度为$a$的所有向量集合。
1-1-4、Vector Elements 向量元素
$y_{i}$ = $i^{th}$ element
通常我们会使用1-索引或者0-索引来表达向量中的某个索引。
$y = \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \end{bmatrix}$ $ y = \begin{bmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \end{bmatrix}$
在数学中,1-索引的情况比较多;但是在机器学习的应用问题中,0-索引为我们提供了一个更方便的符号表达。
1-1-5、一些惯例
通常在书写矩阵和向量时,大多数人会使用大写字母来表示矩阵,比如A、B、C;而通常会使用小写字母来表示数字、标量或者向量,比如a、b、c。
1-2、Addition and Scalar Multiplication 矩阵的加法和标量乘法
1-2-1、Addition 矩阵加法
如果你想将两个矩阵相加,你只需要将这两个矩阵的对应每个元素都逐个相加。
$\begin{bmatrix} 1 & 0 \\ 2 & 5 \\ 3 & 1 \end{bmatrix} + \begin{bmatrix} 4 & 0.5 \\ 2 & 5 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 5 & 0.5 \\ 4 & 10 \\ 3 & 2 \end{bmatrix}$
只有相同维度的两个矩阵才能相加,相加得到的矩阵跟相加的矩阵具有相同的维度。
1-2-2、Scalar Multiplication 矩阵标量乘法
这里的标量可能是一个复杂结构,或者只是一个简单的数字,或者说实数。我们只需要将矩阵中的所有元素都与标量相乘,相乘得到的矩阵跟相乘的矩阵具有相同的维度。
$3 × \begin{bmatrix} 1 & 0 \\ 2 & 5 \\ 3 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 2 & 5 \\ 3 & 1 \end{bmatrix} × 3 = \begin{bmatrix} 3 & 0 \\ 6 & 15 \\ 9 & 3 \end{bmatrix}$
1-2-3、Combination of Operands
$3 × \begin{bmatrix} 1 \\ 4 \\ 2 \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ 5 \end{bmatrix} - \begin{bmatrix} 3 \\ 0 \\ 2 \end{bmatrix} / 3 \\ = \begin{bmatrix} 3 \\ 12 \\ 6 \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ 5 \end{bmatrix} - \begin{bmatrix} 1 \\ 0 \\ \frac{2}{3} \end{bmatrix} \\ = \begin{bmatrix} 2 \\ 12 \\ \frac{31}{3} \end{bmatrix}$
1-3、Matrix Vector Multiplication 矩阵×向量
$\begin{bmatrix} 1 & 3 \\ 4 & 0 \\ 2 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 5 \end{bmatrix} = \begin{bmatrix} 1×1+3×5 \\ 4×1+0×5 \\ 2×1+1×5 \end{bmatrix} = \begin{bmatrix} 16 \\ 4 \\ 7 \end{bmatrix}$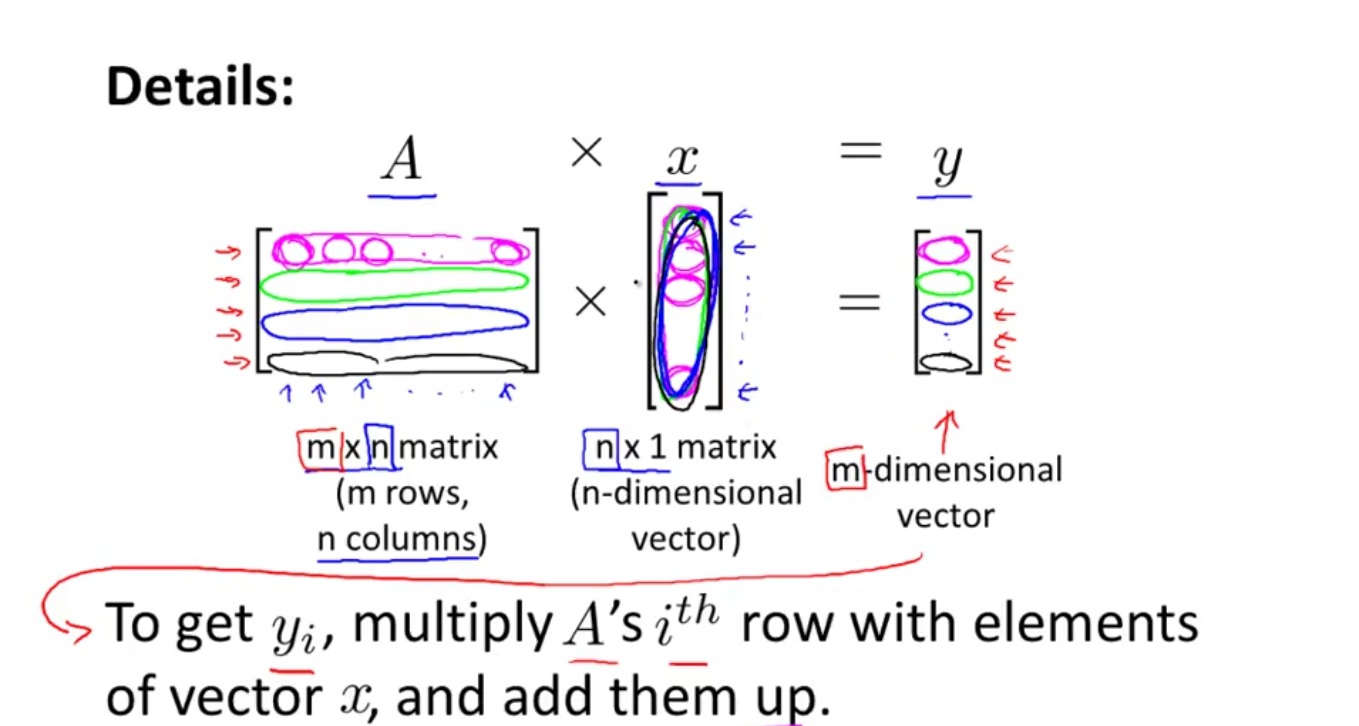
1-4、Matrix Matrix Multiplication 矩阵×矩阵
$\begin{bmatrix} 1 & 3 & 2 \\ 4 & 0 & 1\end{bmatrix} \begin{bmatrix} 1 & 3 \\ 0 & 1 \\ 5 & 2 \end{bmatrix} \\ = \begin{bmatrix} 1×1+3×0+2×5 & 1×3+3×1+2×2 \\ 4×1+0×0+1×5 & 4×3+0×1+1×2\end{bmatrix} \\ = \begin{bmatrix} 11 & 10 \\ 9 & 14 \end{bmatrix}$
乘数矩阵的列数必须与被乘数矩阵的行数一致。

1-5、Matrix Multiplication Properties 矩阵乘法特性
1-5-1、Commutative 交换律
Let $A$ and $B$ be matrices. Then in general, $A \times B \ne B \times A$. (not commutative) 不满足交换律
$\begin{bmatrix} 1 & 1 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} 0 & 0 \\ 2 & 0 \end{bmatrix} = \begin{bmatrix} 2 & 0 \\ 0 & 0 \end{bmatrix}$
$\begin{bmatrix} 0 & 0 \\ 2 & 0 \end{bmatrix} \begin{bmatrix} 1 & 1 \\ 0 & 0 \end{bmatrix} = \begin{bmatrix} 0 & 0 \\ 2 & 2 \end{bmatrix}$
上面两个相乘的矩阵都是方阵($n$×$n$ 矩阵),交换顺序之后才能够相乘。一般情况下,两个矩阵交换顺序甚至不能进行乘法操作。
1-5-2、Associative 结合律
$A \times B \times C = A \times ( B \times C ) $ (Associative) 满足结合律
1-5-3、Identity Matrix 单位矩阵
Denoted $I$ (or $I_{n\times n}$).
单位矩阵是一个方阵,除了主对角线上全是1,其他都是0。
Examples of identity matrices:
$\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$ , $\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$, $\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$
For any matrix $A$, $ A × I = I × A = A$.
For any matrix $A_{n×m}$, $ A_{n×m} × I_{m×m} = I_{n×n} × A_{n×m} = A_{n×m}$.
单位矩阵满足交换律。
1-6、Inverse and Transpose 矩阵的逆运算和转置运算
1-6-1、Matrix Inverse 矩阵的逆运算
Matrix Inverse: if $A$ is an $m \times m$ matrix, and if it has an inverse, $AA^{-1}$ = $A^{-1}A$ = $I$.
一个矩阵有逆矩阵,首先它必须是一个方阵。但是并不是所有的方阵都有自己的逆矩阵,这类没有逆矩阵的方阵叫做奇异矩阵或者退化矩阵。
1-6-2、Matrix Transpse 矩阵的转置运算
$A = \begin{bmatrix} 1 & 2 & 0 \\ 3 & 5 & 9 \end{bmatrix}$ $A^T = \begin{bmatrix} 1 & 3 \\ 2 & 5 \\ 0 & 9 \end{bmatrix} $
Let $A$ be an $m \times n$ matrix, and let $B$ = $A^T$. Then $B$ is an $n \times m$ matrix, and $B_{ij}$ = $A_{ji}$.
矩阵转置运算,即将矩阵按照主对角线翻转。