1、Logistic Regression 逻辑回归
1-1、Introduction 引入
Email: Spam/Not Spam?垃圾邮件分类
Online Transactions: Fraudulent(Yes /No)?网上交易欺诈
Tumor: Malignant/Benign?肿瘤恶性良性
$y\in \{0,1\}$
0: “Negative Class” 负类
1: “Positive Class” 正类
哪个是负类,哪个是正类,有时是任意的,这并不是很重要。通常来说,负类0总是表示缺少某样东西;正类1表示存在某样我们寻找的东西。
很显然,直接使用线性回归算法来解决分类问题不是一个好主意,需要稍微修改。
1-2、Binary Classification Problem 二元分类问题
只有两类输出值0和1的分类问题
1-2-1、Hypothesis Representation 假设表示
我们希望得到一个满足$0\le h_{\theta}(x)\le1$的假设函数
对比线性回归的假设函数$h_{\theta}(x)={\theta}^Tx$,我们不妨做一些修改$h_{\theta}(x)=g({\theta}^Tx)$
并且有$g(z)=\frac{1}{1+e^{-z}}$,这被称为Sigmoid函数或者逻辑函数。
Sigmoid函数图像如下: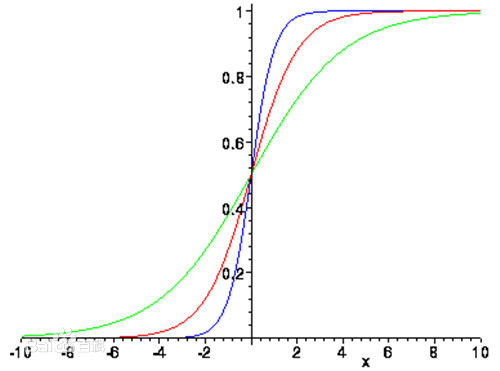
将上面两个式子组合在一起就是我们的假设:
$h_{\theta}(x)=\dfrac{1}{1+e^{-{\theta}^Tx}}$
有了假设函数,和线性回归一样,我们需要做的就是,用参数$\theta$拟合我们的数据。
1-2-2、Interpretation of Hypothesis Output 模型输出解释
$h_{\theta}(x)=$ estimated probability that $y = 1$ on input $x$
当假设函数输出某个数,我们认为这个数是对于新输入样本$x$,$y=1$的概率的估计值。在概率论中,可以表示为$h_{\theta}(x)=p(y=1|x;\theta)$,“probability that y=1 ,given x, parameterized by $\theta$”。
那么,就可以得到下面的式子
$p(y=0|x;\theta)+p(y=1|x;\theta)=1$
$p(y=0|x;\theta)=1-p(y=1|x;\theta)$
1-2-3、Decision Boundary 决策边界
Suppose predict “$y=1$” if $h_{\theta}(x)\ge 0.5$
${\theta}^Tx \ge0$
predict “$y=0$” if $h_{\theta}(x)< 0.5$
${\theta}^Tx < 0$
(如果$y=1$的概率等于0.5,那么可以选择$y=1$,也可以选择$y=0$,这里我们不妨选择了$y=1$)
从Sigmoid函数的图像中我们可以看出:
$g(z)\ge 0.5$, when $z \ge 0$
$( h_{\theta}(x)=g({\theta}^Tx)\ge 0.5$, whenever ${\theta}^Tx\ge 0 )$
$z=0,e^0=1\Rightarrow g(z)=\frac{1}{2}$
$z\rightarrow\infty,e^{-\infty}\rightarrow0\Rightarrow g(z)=1$
$z\rightarrow-\infty,e^{\infty}\rightarrow\infty\Rightarrow g(z)=0$
这样我们可以通过直接计算${\theta}^Tx$的正负性来判断选择$y=1$还是$y=0$,甚至可以通过直接比较函数值大小来得到$y=1$或$y=0$之间的概率高低关系。
而且在任意数量特征值的图上,通过函数关系得到的图像都可以将图一分为二,一部分全部预测为y=1,另一部分全部预测为y=0。不妨以两个特征值为例,两个特征值正好是一副平面图,那么函数关系是一条直线,这条直线将这幅图划分为两部分。
The decision boundary is the line that separates the area where y = 0 and where y = 1. It is created by our hypothesis function.
那么函数关系形成的图像就被称为决策边界(非常形象)。决策边界是假设函数的一个属性,即使我们去掉训练集,这条决策边界也不会改变,决定决策边界的不是训练集,而是假设函数的参数。之后我们会使用训练集计算假设函数的参数,但是一旦参数确定,我们就将完全确定决策边界。
1-2-4、Non-linear Decision Boundaries 非线性决策边界
相当于多项式回归和线性回归的关系,我们也可以尝试去拟合非线性决策边界(使用高阶多项式项),我们可以对逻辑回归使用相同的方法。
比如,$h_{\theta}(x)=g({\theta}_0+{\theta}_1x_1+{\theta}_2x_2+{\theta}_3x_1^2+{\theta}_4x_2^2+\theta_5x_1x_2)$
通过增加复杂的多项式特征变量,我们可以得到更复杂的决策边界,而不仅仅是直线边界。
1-2-5、Cost Function 代价函数
不妨先定义一个代价函数
$Cost(h_{\theta}(x^{(i)}),y^{(i)})=\dfrac{1}{2}(h_{\theta}(x^{(i)})-y^{(i)})^2$
对于这个代价项的理解是,这是我期望的我的学习算法如果想要达到这个值,所需要付出的代价。这个希望的预测值是$h(x)$,而实际值则是y。
我们希望使用梯度下降的算法去解决逻辑回归的参数拟合问题,我们希望代价函数能够是Convex 凸函数(即只有一个局部最小值)。但是很遗憾Sigmoid函数是一个非线性函数,将Sigmoid函数引入代价函数的话,代价函数会变成非凸函数,不满足使用梯度下降算法的条件。因此,我们不能使用前面假设的Cost函数,在逻辑回归上。
综上所述,我们必须重新定义逻辑回归的代价函数
$Cost(h_{\theta}(x),y)=-\log(h_{\theta}(x))$ if $y=1$
$Cost(h_{\theta}(x),y)=-\log(1-h_{\theta}(x))$ if $y=0$
这个函数有很多优秀的性质
$Cost=0$ if $y=1,h_{\theta}(x)=1$
But as $h_{\theta}(x)\rightarrow 0$
$Cost\rightarrow \infty$
Captures intuition that if $h_{\theta}(x)=0,$ (predict $P(y=1|x;\theta)=0$),but $y=1$, we’ll penalize learning algorithm by a very large cost 我们会用很大的代价值来惩罚这个学习算法,因为它将本来是$y=1$的情况分到了$y=0$,而且概率十分离谱。
1-2-6、Simplified Cost Function 简化代价函数
$J(\theta)=\dfrac{1}{m}\displaystyle\sum_{i=1}^mCost(h_{\theta}(x^{(i)}),y^{(i)})$
$Cost(h_{\theta}(x),y)=-\log(h_{\theta}(x))$ if $y=1$
$Cost(h_{\theta}(x),y)=-\log(1-h_{\theta}(x))$ if $y=0$
为了方便书写,最好把上面两个式子合并为一个,这样可以方便地写出代价函数并推导出梯度下降公式
$Cost(h_{\theta}(x),y)=-y\log(h_{\theta}(x))-(1-y)\log(1-h_{\theta}(x))$
这个式子与上面两个式子是完全等价的
这样将单个代价函数代入整体代价函数里面得到
$J(\theta)=\dfrac{1}{m}\displaystyle\sum_{i=1}^mCost(h_{\theta}(x^{(i)}),y^{(i)})\\=-\dfrac{1}{m}\left[\displaystyle\sum_{i=1}^my^{(i)}\log h_{\theta}(x^{(i)})+(1-y^{(i)})\log(1-h_{\theta}(x^{(i)}))\right]$
这个式子是从统计学中的极大似然估计得来的,统计学的思路是如何为不同的模型有效地找出不同的参数,同时它是一个凸函数,可以使用梯度下降算法。
1-2-7、Gradient Descent 梯度下降
$J(\theta)=-\dfrac{1}{m}\left[\displaystyle\sum_{i=1}^my^{(i)}\log h_{\theta}(x^{(i)})+(1-y^{(i)})\log(1-h_{\theta}(x^{(i)}))\right]$
Want ${min}_\theta$ $J(\theta)$
Repeat{
${\theta}_j:={\theta}_j-\alpha\dfrac{\partial}{\partial{\theta}_j}J(\theta)$
} (simultaneously update all $\theta_j$)
这个是我们通常使用的梯度下降算法的模版
通过代入计算的偏导数,可以得到一个新的式子
${\theta}_j:={\theta}_j-\dfrac{\alpha}{m}\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}$
Alogorithm looks identical to linear regression!
这个式子正是我们用来做线性回归梯度下降,两个式子是完全一模一样的。但是由于假设函数发生了变化,所以逻辑回归的梯度下降跟线性回归的梯度下降实际上是两个完全不同的东西。
监控梯度下降算法以确保其收敛,这在逻辑回归中也是适用的。
当然需要使公式向量化来简化运算。特征缩放也适用于逻辑回归,如果你的特征范围差距很大的话,使用特征缩放也可以使得收敛速度加快。
向量化实现:
$h=g({\theta}^Tx)$
$J(\theta)=\frac{1}{m}(-y^T\log(h)-(1-y)^T\log(1-h))$
$\theta:=\theta-\frac{\alpha}{m}X^T(g({\theta}^Tx)-y)$
1-2-8、偏导数推倒过程
简单推导一下偏导数的求解过程
$J({\theta})=-\dfrac{1}{m}\displaystyle\sum_{i=1}^m\left[y^{(i)}\ln h_\theta(x^{(i)})+(1-y^{(i)})\ln(1-h_\theta(x^{(i)}))\right]$
为了书写方便和递推简单,不妨设$h_\theta(x^{(i)})=\dfrac{1}{1+e^{-z}}$,$z={\theta}^Tx$
$\dfrac{\partial J(\theta)}{\partial\theta_j}=-\dfrac{1}{m}\displaystyle\sum_{i=1}^m\left[y^{(i)}\dfrac{e^{-z}x_j^{(i)}}{h_\theta(x^{(i)})(1+e^{-z})^2}+(1-y^{(i)})\dfrac{-e^{-z}x_j^{(i)}}{(1-h_\theta(x^{(i)}))(1+e^{-z})^2}\right]\\=-\dfrac{1}{m}\displaystyle\sum_{i=1}^m\left[\dfrac{e^{-z}x_j^{(i)}}{(1+e^{-z})^2}\left(\dfrac{y^{(i)}}{h_\theta(x^{(i)})}+\dfrac{y^{(i)}-1}{1-h_\theta(x^{(i)})}\right)\right]\\=-\dfrac{1}{m}\displaystyle\sum_{i=1}^m\left[\dfrac{e^{-z}x_j^{(i)}}{(1+e^{-z})^2}\left(y^{(i)}(1+e^{-z})+(y^{(i)}-1)\dfrac{1+e^{-z}}{e^{-z}}\right)\right]\\=-\dfrac{1}{m}\displaystyle\sum_{i=1}^m\left[\dfrac{x_j^{(i)}}{(1+e^{-z})^2}\left(y^{(i)}(1+e^{-z})e^{-z}+(y^{(i)}-1)(1+e^{-z})\right)\right]\\=-\dfrac{1}{m}\displaystyle\sum_{i=1}^m\left[\dfrac{x_j^{(i)}}{(1+e^{-z})^2}\left(y^{(i)}(1+e^{-z})^2-(1+e^{-z})\right)\right]\\=-\dfrac{1}{m}\displaystyle\sum_{i=1}^m\left[x_j^{(i)}\left(y^{(i)}-\dfrac{1}{1+e^{-z}}\right)\right]\\=-\dfrac{1}{m}\displaystyle\sum_{i=1}^m\left(y^{(i)}-h_\theta(x^{(i)})\right)x_j^{(i)}\\=\dfrac{1}{m}\displaystyle\sum_{i=1}^m\left(h_\theta(x^{(i)})-y^{(i)}\right)x_j^{(i)}$
1-3、Advanced Optimization 高级优化
Optimization algorithm 优化算法:
- Gradient descent 梯度下降
- Conjugate gradient 共轭梯度法
- BFGS 变尺度法
- L-BFGS 限制变尺度法
除了梯度下降算法,还有其他方法求解使得代价函数最小的参数$\theta$。
这里只做最基本的介绍,简单说说他们的优缺点:下面三种算法有许多优点,(1)不需要手动选择学习率$\alpha$,他们有一种叫line search 线性搜索的算法,它可以自动尝试不同的学习速率$\alpha$并且选择一个; (2)收敛速度远远快于梯度下降算法;缺点:他们比梯度下降算法复杂多了。
Example
$\theta=
\begin{bmatrix}
\theta_1 \\
\theta_2
\end{bmatrix}
$
$J(\theta)=(\theta_1-5)^2+(\theta_2-5)^2$
$\dfrac{\partial}{\partial\theta_1}J(\theta)=2(\theta_1-5)$
$\dfrac{\partial}{\partial\theta_2}J(\theta)=2(\theta_2-5)$
调用高级优化函数
fminunc是Octave里无约束最小化函数。
options是作为一个数据结构可以存储你想要的options,
‘GradObj’、‘on’表示设置梯度目标参数为打开,这意味着你现在确实要给这个算法提供一个梯度;‘100’、‘MaxIter’表示最大迭代次数为100次。
给出一个$\theta$的猜测初始值initialTheta,@表示指向我们刚刚定义的costfunction函数的指针。
如果调用这个函数,那么软件就会使用众多高级优化算法中的一个。当然你也可以把它当作梯度下降算法,只不过它可以自动选择$\alpha$,而不需要自己选择。
逻辑回归的高级优化
$\theta=
\begin{bmatrix}
\theta_0 \\
\theta_1 \\
. \\
. \\
. \\
\theta_n
\end{bmatrix}
$
我们需要做的是写一个函数,它能返回代价函数值以及梯度值,我们可以把这个优化函数运用到逻辑回归,甚至是线性回归中。我们需要做的就是,写入合适的代码,来计算这里的东西。
有个这个算法,我们可以使用一个复杂的优化库,它虽然让算法更加模糊一点难以调试。但是由于这个算法的运行速度远远快于梯度下降,因此每当有一个大规模学习问题的时候,都可以使用。
1-4、Multiclass Classification 多类别分类问题
Examples
Email foldering/tagging: Work, Friends, Family, Hobby
Medical diagrams: Not ill, Cold, Flu
Weather: Sunny, Cloudy, Rain, Snow
One-vs-all 一对多
不妨设我们现在有y=1,y=2,y=3这三类输出值的一个多类别分类问题。我们需要做的就是把这个问题分成三个二元分类问题。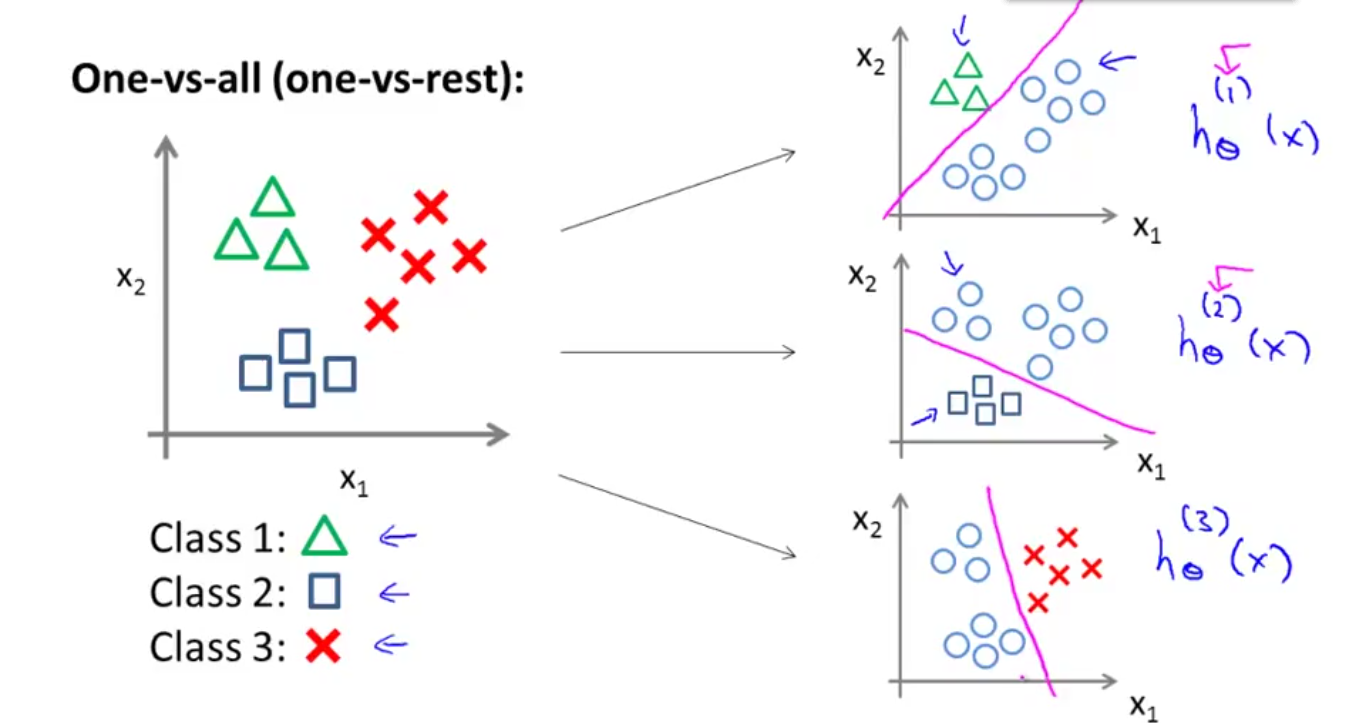
这样就可以得到:
$h_{\theta}^{(i)}(x)=P(y=i|x;\theta)$ $(i=1,2,3)$
这样分别计算每一个分类器的概率是多少,并判断大小关系即可。
Train a logistic regression classifier $h_{\theta}^{(i)}(x)$ for each class $i$ to predict the probability that $y=i$.
On a new input $x$, to make a prediction, pick the class $i$ that maximizes $h_{\theta}^{(i)}(x)$.
2、Regularization 正则化
2-1、回归可能存在的情况
2-1-1、Undrefitting 欠拟合(High Bias 高偏差)
Underfitting, or high bias, is when the form of our hypothesis function h maps poorly to the trend of the data. It is usually caused by a function that is too simple or uses too few features.
从图形上看,拟合曲线不能很好地拟合训练数据,那么我们把这个问题叫做Underfitting 欠拟合,也可以叫做High bias 高偏差。这两种说法大致相同,意思是假设函数没有很好的拟合训练数据。
如果拟合一条直线到训练数据,但是算法有一个很强的偏见或者说一个很大的偏差,因为该算法认为房子的价格与面积仅仅线性相关,尽管与该数据的事实相反,尽管相反的事实被事前定义为偏差,它还是接近于拟合一条直线,而此法最终导致拟合数据的效果很差。
上面是视频的原话,说句实话翻译得非常烂,我这里用自己的话说说我的理解。在预测房价的问题上,如果勉强去使用直线去拟合训练数据,也是可以成功的,但是实际情况下房价与面积很显然不是呈线性关系那么简单。那么拟合出来的结果的可行度就是值得怀疑的,因为在拟合数据之前,你已经规定了(确信)特征值(房屋面积)与输出值(房价)是线性相关的,最后预测结果出现偏差也是很正常的。
2-1-2、Overfitting 过度拟合
Overfitting, or high variance, is caused by a hypothesis function that fits the available data but does not generalize well to predict new data. It is usually caused by a complicated function that creates a lot of unnecessary curves and angles unrelated to the data.
所用的假设函数能够几乎很好的拟合所有训练数据,但是这个曲线很显然与事实情况完全不符,那么我们称这个问题为过度拟合或者high variance 高方差。
如果我们拟合一个高阶多项式,而且这个函数可以很好的拟合训练集,能拟合几乎所有的训练数据,这就面临着可能函数太过庞大、变量太多的问题,同时我们没有足够的数据去约束这个变量过多的模型,那么这就是过度拟合。
简单的理解一下,就是我们找到一个变量过多的函数模型,可以很好的拟合所提供的训练集,但是因为训练集的有限,可能会导致在训练集范围这个函数是合理的、有效的,但是在训练集之外的范围可能会导致与事实不符的输出值。
If we have too many features, the learned hypothesis may fit the trainning set very well ( $J(\theta)=\dfrac{1}{2m}\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^2\approx0$), but fail to generalize to new examples(predict prices on new examples).
如果假设函数千方百计的拟合于训练数据,这样导致它无法泛化到新的数据样本中,以至于无法预测新的样本价格。
generalize 泛化:泛化指的是一个假设模型能够应用到新样本的能力
2-1-3、Just Right 刚好合适
在欠拟合和过度拟合之间,那么就肯定存在刚好合适的情况,即兼顾曲线拟合训练数据又兼顾预测新数据的能力的情况。
2-2、Addressing Overfitting 解决过度拟合问题
当我们使用一维或者两维数据的时,我们可以通过绘制假设函数模型的图像来研究问题所在,再选择合适的多项式来拟合数据。因此绘制假设函数模型曲线,可以作为决定高阶多项式的一种方法,但是这并不是总是有用的。
当我们有许多特征量的时候,多维度使得绘图也变得非常困难,并且使得其难以可视化。因此并不能通过这种方法来决定保留那些特征变量。
Reduce number of featrues 减少特征变量的数量
-Manually select which features to keep 人工检查变量的条目并以此决定哪些变量更为重要,然后决定保留哪些变量,哪些应该舍弃。
-Model selection algorithm 模型选择算法(之后会提到)
这种算法可以自动选择采用哪些变量,自动舍弃不需要的变量。
优点:这种做法是非常有效的,并且可以减少过度拟合的发生。
缺点:舍弃一部分特征变量,你也舍弃了问题中的一些信息。比如,也许所有的特征变量对于预测房价都是有用的,我们实际上并不想舍弃一些信息或者舍弃这些特征变量。
Regularization 正则化
-Keep all the features, but reduce magnitude/values of parameters ${\theta}_j$
保留所有特征变量,但是会减小数量级或者参数${\theta}_j$数值的大小
-Regularization works well when we have a lot of slightly useful features.
当我们有很多特征变量的时候,其中每一个变量都能对预测产生一点影响,所以保留所有特征值是很有必要的。
2-3、Cost Function 代价函数
在使用正则化的时候,我们会使用新的代价函数
对原来的代价函数添加一些对${\theta}_3,{\theta}_4$的惩罚项
比如代价函数$J(\theta)=\dfrac{1}{2m}\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^2+1000{{\theta}_3}^2+1000{{\theta}_4}^2$,此时如果我们需要最小化这个新的代价函数,我们要让${\theta}_3$和${\theta}_4$尽可能的小,那么最后${\theta}_3,{\theta}_4$应该接近于0,就像我们在假设函数中忽略了这两个值一样。
在这个代价函数中,我们有惩罚这两个大的参数值的效果。
2-4、Regularization 正则化
Small values of parameters ${\theta}_0,{\theta}_1,…,{\theta}_n$
-“Simpler” hypothesis 更简单的假设函数
-Less prone to overfitting 发生过度拟合的可能性更小
如果我们的参数值比较小(不妨把这个参数值看做0,不妨把这一项看成没有),那么往往我们会得到一个形式更简单的假设。
也对应于越光滑、越简单的函数,因此也就越不易发生过度拟合的情况。
当特征变量过多的时候,我们是很难提前选出那些关联度更小的特征的,如何缩小参数的数目是很难的。
那么,不妨缩小所有的参数值
$J(\theta)=\dfrac{1}{2m}\left[\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^2+\lambda\displaystyle\sum_{i=1}^n{\theta}_i^2\right]$
通过添加这个额外的正则化项,我们收缩了每个参数。
这里有一个注意点,我们没有去惩罚${\theta}_0$,因此${\theta}_0$的值是最大的,这是一个约定。在实践中,这样做只会有非常小的差异,这里仅仅是为了简便或者是因为惯例。
我们现在的优化目标是$min J(\theta)$,最小化新的代价函数。这里的$\lambda$被称为Regularization Parameters 正则化参数,$\lambda$要做的就是达到在两个目标之间的平衡关系,一个目标就是我们想要使假设函数更好地拟合训练数据,能够很好的适应训练集;另一个目标是我们想要保持参数值较小,使得假设函数没有过度拟合训练数据。
总结的说,$\lambda$的目标就是平衡拟合训练集的目的和保持参数值较小的目的,从而保持假设函数形式的相对简单,来避免过度的拟合。
如果$\lambda$过大的话,我们将会非常大地惩罚所有参数,那么所有参数都会接近于0。这样的话,我们相当于用一条水平直线去拟合数据,这样很显然就是欠拟合的情况。也可以这么说,这种假设函数有过于强烈的“偏见”或者过高的偏差。
如果$\lambda$过小的话,我们将几乎不会惩罚参数,那么所有参数可以根据训练集“随意”变大变小。这样的话,假设函数会强行曲折去匹配训练数据,这样就是过度拟合的情况。
为了使正则化运行良好,我们应该去选择一个适当的正则化参数$\lambda$。
2-5、Regularized Linear Regression 正则化线性回归
在这一节,我们将梯度下降和正规方程推广到正则化线性回归中。在代价函数中添加了新的一项后,我们解决线性回归的方法也需要修改。
2-5-1、梯度下降推广
在正则化中,因为约定我们不会惩罚${\theta}_0$,所以在梯度下降算法中需要将$n=0$的情况列出来并且保持不变。
Repeat{
${\theta}_0:={\theta}_0-\alpha\dfrac{1}{m}\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})x_0^{(i)}$
${\theta}_j:={\theta}_j-\alpha\left[\dfrac{1}{m}\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}+\dfrac{\lambda}{m}{\theta}_j\right]$
}
上面这个新的梯度下降的公式就可以用于最小化正则化代价函数。
仔细观察上式,我们可以化简第二个式子:
${\theta}_j:={\theta}_j(1-\alpha\dfrac{\lambda}{m})-\dfrac{\alpha}{m}\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}$
观察${\theta}_j$的参数项$(1-\alpha\dfrac{\lambda}{m})$,很显然可以得到下面这个不等式$1-\alpha\dfrac{\lambda}{m}< 1$
所以我们通常可以知道$(1-\alpha\dfrac{\lambda}{m})$是一个比1小一点点的值,不妨将它想象成0.99的数。所以对更新公式可以理解为${\theta}_j$被替换为${\theta}_j$的0.99倍,之后的第二项与原来的更新一样。
公式总结
代价函数
$$J(\theta)=\dfrac{1}{2m}\left[\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^2+\lambda\displaystyle\sum_{i=1}^n{\theta}_i^2\right]$$
梯度下降公式
Repeat{
${\theta}_0:={\theta}_0-\alpha\dfrac{1}{m}\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})x_0^{(i)}$
${\theta}_j:={\theta}_j(1-\alpha\dfrac{\lambda}{m})-\dfrac{\alpha}{m}\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}$
}
2-5-2、正规方程推广
同样正规方程的公式也需要改变
$\theta=(X^TX+\lambda\left[
\begin{matrix}
0& 0& 0& \dots& 0\\
0& 1& 0& \dots& 0\\
0& 0& 1& \dots& 0\\
.& .& .& \dots& .\\
.& .& .& \dots& .\\
0& 0& 0& \dots& 1
\end{matrix}
\right])^{-1}X^Ty$
公式中的矩阵显然应该是$(n+1)(n+1)$的矩阵。
*不可逆性
这里简单的说说正则化正规方程不可逆性的问题。
假如 $m\le n$,
$(X^TX)^{-1}$肯定是一个不可逆矩阵。
幸运的是,只要正则化参数是严格大于0的话,可以证明$\theta=(X^TX+\lambda\left[
\begin{matrix}
0& 0& 0& \dots& 0\\
0& 1& 0& \dots& 0\\
0& 0& 1& \dots& 0\\
.& .& .& \dots& .\\
.& .& .& \dots& .\\
0& 0& 0& \dots& 1
\end{matrix}
\right])^{-1}X^Ty$一定是可逆的。
也就是说正则化还可以将一些优化前不可逆的问题转化为可逆的问题。
2-6、Regularized Logistic Regression 正则化逻辑回归
同样,我们需要把梯度下降和高级优化推广到正则化逻辑回归上。
2-6-1、梯度下降推广
我们需要修改代价函数
$J(\theta)=-\left[\dfrac{1}{m}\displaystyle\sum_{i=1}^my^{(i)}\log h_{\theta}(x^{(i)})+(1-y^{(i)})\log(1-h_{\theta}(x^{(i)}))\right]+\dfrac{\lambda}{2m}\displaystyle\sum_{j=1}^n{\theta}_j^2$
那么对于梯度下降公式,我们也需要做出相应的变化(与正则化线性回归梯度下降公式一样)
Repeat{
${\theta}_0:={\theta}_0-\alpha\dfrac{1}{m}\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})x_0^{(i)}$
${\theta}_j:={\theta}_j(1-\alpha\dfrac{\lambda}{m})-\dfrac{\alpha}{m}\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}$
}
这里两个算法不是完全一样的,因为假设函数是不一样的。
2-6-2、高级优化推广
|
|
高级优化的基本结构与前面一样,只不过计算$J(\theta)$和梯度的公式稍微变化了一点,其它没有变化。