PCA(Principal Component Analysis)是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降维。
这篇文章的目的是记录我学习PCA过程的心得体会,介绍一下PCA的基本数学原理,文章有错误的地方欢迎指正。
降维以减小复杂度
在数据挖掘和机器学习中,数据用向量表示,一条记录可以是一个$n$维列向量。比如某淘宝店一天的营业情况可以表示如下:
$$(浏览量,访客数,下单数,成交数,成交金额)^T$$
这里使用了转置符号,因为习惯上使用列向量来表示一条记录,下文默认所提及向量都是列向量。
我们知道,大多数机器学习算法的复杂度是和数据的维度相关的,甚至可以是呈指数级关系。这里我们的数据仅是五维,也许无所谓,但是在实际的数据挖掘问题中,几百上千维的数据并不罕见。在这种情况下,处理数据所使用的时间资源是我们无法承受的,所以我们必须对数据进行降维。
原始数据的每一维度并不一定是不可或缺的,有些维度是冗余的,比如身高以米为单位,和身高以英尺为单位,这两个特征量是存在明显的换算关系的。进行数据挖掘的时候只需要其中的一个即可,删除任何一个不会导致信息损失;在极限情况下,可能每一维度都是不冗余的,对算法来说都是重要的,但是在同样重要的情况下还是可以分出一个先后次序,舍弃相对来说不是那么重要的维度就成了降维的可能手段。
上面说的例子可能有点极端,我们重新来看淘宝店的例子。从经验上看,我们猜想“浏览量”和“访客数”可能具有一定的关系,而“下单数”和“成交数”也会具有一定的关系。它们之间不一定有一种可以通过公式来表达的线性关系,但是毫无疑问,当一天的“浏览量”很大的时候,我们很大程度上可以认定当天的“访客数”也很大。
在这种情况下,我们可以考虑删除“浏览量”和“访客数”其中的一个指标,这样既可以保证信息的损失很小,又可以降低机器学习算法的复杂度。
上面这种情况,只是直观地表达了降维的动机和可行性,并没有实际上的可操作性。到底删除哪一列?哪些列之间有上述所说的相关性?是删除一列还是删除几列?亦或是通过某些操作变换效果更佳?这些问题都需要PCA的计算才能得到答案。
向量变换
介绍向量变换的相关知识,以此作为推导PCA的理论基础。
内积与投影
两个维度相同的向量的内积被定义为:
$$(a_1,a_2,\dots,a_n)^T\cdot(b_1,b_2,\dots,b_n)^T=a_1b_1+a_2b_2+\cdots+a_nb_n$$
内积运算将两个向量映射为一个实数。分析内积的几何意义,假设$A$和$B$是两个$n$维向量,我们知道$n$维向量可以等价表示为$n$维空间中的一条从原点引出的有向线段。为了简单起见,我们假设$A$和$B$均为二维向量,则$A=(x_1,y_1)$,$B=(x_2,y_2)$。在二维平面上$A$和$B$可以用两条从原点引出的有向线段表示,如下图: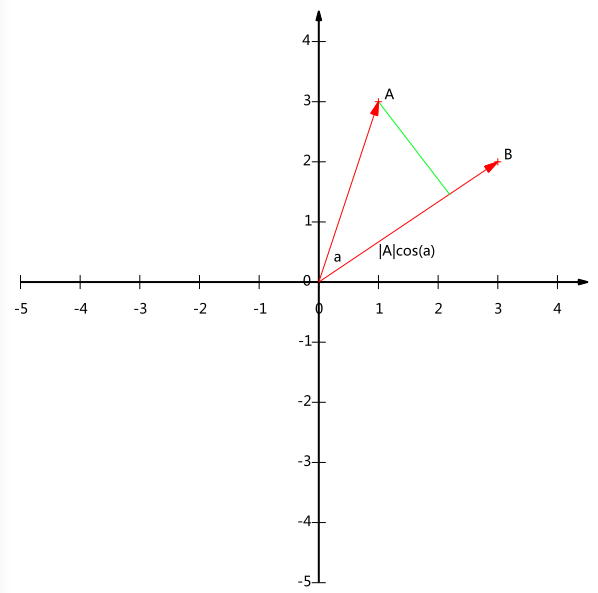
我们从$A$点向$B$点所在直线引一条垂线。垂线与直线$B$的交点叫做点$A$在直线$B$上的投影点,再设直线$A$与直线$B$的夹角是$a$,则投影长为$|A|cos(a)$,其中$|A|=\sqrt{x_1^2+y_1^2}$是向量$A$的模。
将内积表示为另一形式:
$$A\cdot B=|A||B|cos(a)$$
$A$与$B$的内积等于$A$到$B$的投影长度乘以$B$的模。再进一步,假设$B$的模是1,即$|B|=1$,那么:
$$A\cdot B=|A|cos(a)$$
也就是说,设向量$B$的模为1,则$A$与$B$的内积值等于$A$向$B$所在的直线投影的矢量长度!这是一个重要结论,后面的推导会反复用到这个结论。
基
随意给出一个二维向量(3,2),如下图: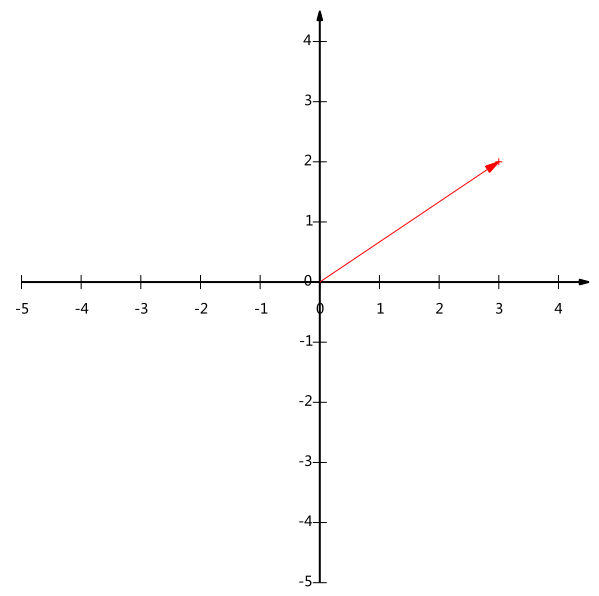
在代数表示方面,我们经常用线段终点的点坐标表示向量,这是我们再熟悉不过的向量表示方式。
我们常常忽略,只有一个(3,2)本身是不能够精确表示一个向量的。这里的3实际表示的是向量在x轴上的投影值是3,在y轴上的投影值是2。也就是说我们其实隐式地引入了一个定义:以x轴和y轴上正方向长度为1的向量为基。那么一个向量为(3,2)实际是说在x轴上投影为3而在y轴的投影为2。
更加正式的说,向量(x,y)实际上表示线性组合:
$$x(1,0)^T+y(0,1)^T$$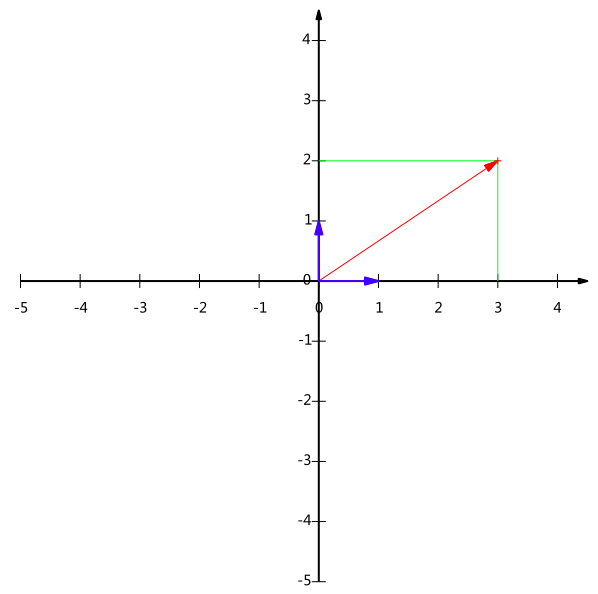
所以,要准确地描述向量,首先要确定一组基,然后给出向量在基所在的各个直线上的投影值。
我们之所以默认选择(1,0)和(0,1)为基,当然是因为方便,二维平面上点坐标和向量是一一对应的。但是实际上任何两个线性无关的二维向量都可以成为一组基,比如(1,1)和(-1,1)。一般来说,我们希望基的模是1。因为从内积的性质上看,如果基的模是1的话,我们可以通过内积计算很简便地得到坐标。实际上,我们可以通过向量除以它的模来得到一个模为1的基,上面的基可以变为$(\frac{1}{\sqrt2},\frac{1}{\sqrt2})$和$(\frac{1}{\sqrt2},-\frac{1}{\sqrt2})$。
通过内积计算,我们可以得到(3,2)在新基$(\frac{1}{\sqrt2},\frac{1}{\sqrt2})$和$(\frac{1}{\sqrt2},-\frac{1}{\sqrt2})$上的坐标是$(\frac{5}{\sqrt2},-\frac{1}{\sqrt2})$。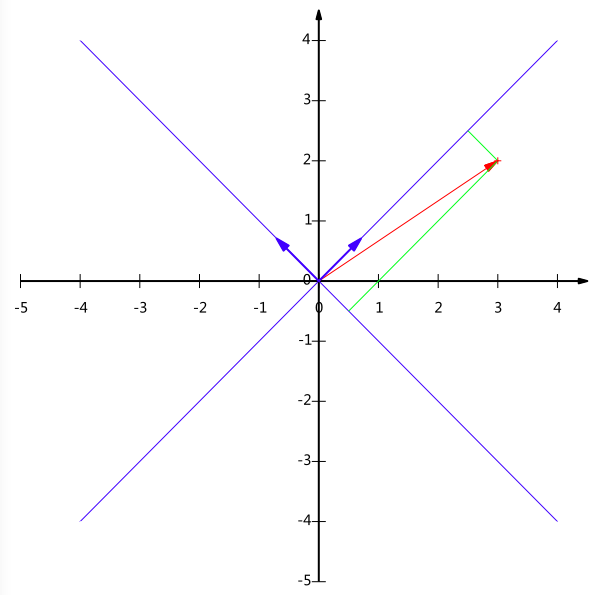
基还有一种特殊情况是正交基,正交基有很多较好的性质,所以很多时候我们会选择正交基作为我们的新基。
基变换
下面介绍一下基变换。我们可以使用矩阵相乘的形式简洁地表示基变换:
$$
\begin{pmatrix}
\frac{1}{\sqrt2} & \frac{1}{\sqrt2} \\\
-\frac{1}{\sqrt2} & \frac{1}{\sqrt2}
\end{pmatrix}
\begin{pmatrix}
3 \\\
2
\end{pmatrix} =
\begin{pmatrix}
\frac{5}{\sqrt2} \\\
-\frac{1}{\sqrt2}
\end{pmatrix}
$$
一般的,如果我们有$M$个$N$维向量,想将其变换为由$R$个$N$维向量表示的新空间中,那么首先将$R$个基按行组成矩阵$A$,然后将向量按列组成矩阵$B$,那么两矩阵的乘积$AB$就是变换结果,其中$AB$的第$m$列为$A$中的第$m$列变换后的结果。
$$
\begin{pmatrix}
p_1 \\\
p_2 \\\
\vdots \\\
p_R
\end{pmatrix}
\begin{pmatrix}
a_1 & a_2 & \dots & a_M
\end{pmatrix} =
\begin{pmatrix}
p_1a_1 & p_1a_2 & \cdots & p_1a_M \\\
p_2a_1 & p_2a_2 & \cdots & p_2a_M \\\
\vdots & \vdots & \ddots & \vdots \\\
p_Ra_1 & p_R a_2 & \cdots & p_Ra_M
\end{pmatrix}
$$
其中$p_i$是一个行向量,表示第$i$个基,$a_j$是一个列向量,表示第$j$个原始数据。
这里$R$是可以小于$N$的,而且$R$决定了变换后数据的维数。也就是说,我们可以将一个$N$维数据变换到更低维度的空间中去,变换后的维度取决于基的数量。因此这种矩阵相乘的表示也可以表示降维变换。
上述分析同时给矩阵相乘找到了一种物理解释:两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去。更抽象的说,一个矩阵可以表示一种线性变换。
协方差矩阵及优化
我们实现了降维的计算方法,还需要解决如何选择基的问题。或者说,如果我们有一组$N$维向量,现在要将其降到$K$维($K$小于$N$),那么我们应该如何选择$K$个基才能最大程度保留原有的信息?
假设我们的数据有五条,将它们表示成矩阵形式:
$$
\begin{pmatrix}
1 & 1 & 2 & 4 & 2 \\\
1 & 3 & 3 & 4 & 4
\end{pmatrix}
$$
为了后续处理方便,我们首先将每个字段内所有值都减去字段均值,其结果是:
$$
\begin{pmatrix}
-1 & -1 & 0 & 2 & 0 \\\
-2 & 0 & 0 & 1 & 1
\end{pmatrix}
$$
放到二维平面中:
这个问题实际上是要在二维平面中选择一个方向,将所有数据都投影到这个方向所在直线上,用投影值表示原始记录,而且保留的信息最多。那么如何选择方向(基)才能尽可能保留最多的原始信息呢?一种直观的看法是:希望投影值能够尽可能分散。
方差
上面说到的分散可以用方差来衡量。
$$Var(a)=\dfrac{1}{m}\sum_{i=1}^m(a_i-\mu)^2$$
由于上面我们已经将所有字段的均值都化为0了,因此:
$$Var(a)=\dfrac{1}{m}\sum_{i=1}^ma_i^2$$
上面的问题就被形式化为:寻找一个一维基,使得所有数据变换为这个基上的坐标表示后,方差值最大。
协方差
对于二维降成一维的情况,如上所说。不过对于更高维,还需要解决一个问题。考虑三维降到二维的问题,首先我们需要找到一个方向使得投影后方差最大,这样就完成了第一个方向的选择,继而需要选择第二个方向。
如果我们还是选择方差最大的方向,很明显,这个方向与第一个方向应该是完全重合的。这样做是没有意义的,需要加约束条件。从直观上,让两个字段尽可能表示更多的原始信息,我们是不希望它们之间存在(线性)相关性的,因为相关性意味着两个字段不是完全独立的,必然存在重复表示的信息。
数学上可以用两个字段的协方差表示其相关性:
$$Cov(a,b)=\dfrac{1}{m}\sum_{i=1}^m(a_i-\mu_a)(b_i-\mu_b)$$
由于上面我们已经将所有字段的均值都化为0了:
$$Cov(a,b)=\dfrac{1}{m}\sum_{i=1}^ma_ib_i$$
在字段均值为0的情况下,两个字段的协方差简洁的表示为其内积除以$m$。
当协方差为0时,表示两个字段完全独立。为了让协方差为0,我们选择第二个基时只能在与第一个基正交的方向上选择。
我们进一步得到了降维问题的优化目标:将一组$N$维向量降为$K$维($0<K<N$),其目标是选择$K$个单位正交基,使得原始数据变换到这组基上,各字段两两间协方差为0,而字段的方差则尽可能大(在正交的约束下,取最大的$K$个方差)。
协方差矩阵
假设只有$a$和$b$两个字段,组成矩阵$X$:
$$X=
\begin{pmatrix}
a_1 & a_2 & \cdots & a_m \\\
b_1 & b_2 & \cdots & b_m
\end{pmatrix}
$$
然后用$X$乘以$X$的转置,并乘上系数:
$$
\frac{1}{m}XX^T=
\begin{pmatrix}
\frac{1}{m}\sum_{i=1}^ma_i^2 & \frac{1}{m}\sum_{i=1}^ma_ib_i \\\
\frac{1}{m}\sum_{i=1}^ma_ib_i & \frac{1}{m}\sum_{i=1}^mb_i^2
\end{pmatrix}
$$
这个矩阵对角线上的两个元素分别是两个字段的方差,其它元素是$a$和$b$的协方差。
一般的,设我们有$m$个$n$维数据记录,将其排列$n$乘$m$的矩阵,设$C=\frac{1}{m}XX^T$,则$C$是一个对称矩阵,其对角线分别表示各个字段的方差,而第$i$行$j$列,表示$i$和$j$字段的协方差。
协方差矩阵对角化
根据上述推导,我们发现要达到优化目标,等价于将协方差矩阵对角化。
设原始数据矩阵$X$对应的协方差矩阵为$C$,而$P$是一组基按行组成的矩阵,设$Y=PX$,则$Y$为$X$对$P$做基变换后的数据。设$Y$的协方差矩阵为$D$,推导一下$D$和$C$的关系:
$$
\begin{array} {l l l}
D & = & \frac{1}{m}YY^T \\\
& = & \frac{1}{m}(PX)(PX)^T \\\
& = & \frac{1}{m}PXX^TP^T \\\
& = & P(\frac{1}{m}XX^T)P^T \\\
& = & PCP^T
\end{array}
$$
我们要找的P就是能让原始协方差矩阵对角化的P。换句话说,优化目标变成了寻找一个矩阵$P$,满足$PCP^T$是一个对角矩阵,并且对角元素从大到小依次排序,那么$P$的前$K$行就是要寻找的基,用$P$的前$K$行组成的矩阵乘以$X$就使得$X$从$N$维降到了$K$维并满足上述条件。
从数学上,我们知道一个$n$行$n$列的实对称矩阵一定可以找到$n$个单位正交特征向量,设这$n$个特征向量为$e_1,e_2,\dots,e_n$,我们将其按列组成矩阵:
$$E=
\begin{pmatrix}
e_1 & e_2 & \dots & e_n
\end{pmatrix}
$$
则对协方差矩阵$C$有如下结论:
$$
E^\mathsf{T}CE=\Lambda=\begin{pmatrix}
\lambda_1 & & & \\\
& \lambda_2 & & \\\
& & \ddots & \\\
& & & \lambda_n
\end{pmatrix}
$$
其中$\Lambda$为对角矩阵,其对角矩阵为各特征向量对应的特征值
我们已经找到了需要的矩阵$P$:
$$P=E^T$$
算法
PCA算法
总结一下PCA的算法步骤:
设有$m$条$n$维数据
1)将原始数据按列组成$n$行$m$列矩阵$X$
2)将$X$的每一行(代表每一个属性字段)进行零均值化,即减去这一行的均值
3)求出协方差矩阵$C=\frac{1}{m}XX^T$
4)求出协方差矩阵的特征值及对应的特征向量
5)将特征向量按对应特征值大小从上到下按行排列成矩阵,取前$k$行组成矩阵$P$
6)$Y=PX$即为降维到$k$维后的数据
关键代码
|
|
完整代码请点击shengtao96-github-pca.py
进一步讨论
根据上面对PCA的数学原理的解释,我们可以了解到一些PCA的能力和限制。PCA本质上是将方差最大的方向作为主要特征,并且在各个正交方向上将数据“离相关”,也就是让它们在不同正交方向上没有相关性。
因此,PCA也存在一些限制,例如它可以很好的解除线性相关,但是对于高阶相关性就没有办法了,对于存在高阶相关性的数据,可以考虑Kernel PCA,通过Kernel函数将非线性相关转为线性相关,关于这点之后会进行相关讨论。另外,PCA假设数据各主特征是分布在正交方向上,如果在非正交方向上存在几个方差较大的方向,PCA的效果就大打折扣了。
最后需要说明的是,PCA是一种无参数技术,也就是说面对相同的数据,如果不考虑清洗,谁来做结果都是一样,没有主观参数的介入,所以PCA便于通用实现,但是本身无法个性化的优化。