LDA(Linear Discriminant Analysis,线性判别分析)是一种常用的数据分析方法,也叫做Fisher线性判别(Fisher Linear Discriminant)。LDA算法的目标也是降维,它在降维的同时保留的是类别的区别信息。
1、问题
当我们使用PCA算法降维时,并没有考虑类别标签的因素,属于无监督的。在监督学习中使用PCA算法,往往可能使得分类器更加难以建立。因为PCA算法在降维的时候没有充分利用标签信息,虽然成功的降维了但是损失了关联性。在数据往主成分方向投影后,本来可以建立分类器的数据,很大可能多个类别混在一起,如下图左图: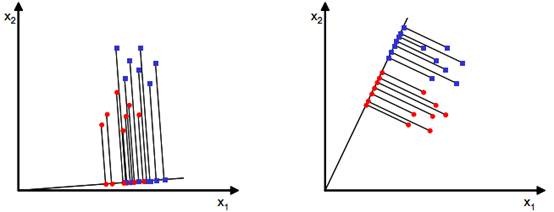
2、二类情况
我们先考虑二值分类情况,也就是$y_i=0$或者$y_i=1$。
我们先来定义问题:给定特征为$d$维的$N$个样本,按列组成矩阵$X=\begin{bmatrix}x_1 & x_2 & \dots & x_N\end{bmatrix}$,其中有$N_1$个样本属于类别$\omega_1$,另外$N_2$个样本属于类别$\omega_2$。我们想将$d$维数据降维到只有一维,而且又要保证能够“清晰”地分辨投影后的两类数据。
我们需要找到这个最佳向量$w$(因为最后降维到一维,所以需要寻找的不是一组基(矩阵)$W$,而是一个$d$维列向量$w$),将原始数据投影到新的方向上$w^Tx_i$,而且最好可以通过一个阈值来分辨这两类数据。如上图右图。
我们需要定量的找到这一向量$w$。
首先我们确定每类样本的均值(中心点)
$$\mu_i=\dfrac{1}{N_i}\displaystyle\sum_{x_i\in \omega_i}x_i$$
而且$x_i$投影到$w$之后的样本的均值为
$$\tilde \mu_i=\dfrac{1}{N_i}\displaystyle\sum_{x_i\in\omega_i}w^Tx_i=w^T\mu_i$$
由此可知,投影后的均值也就是样本中心点的投影。
什么样的向量是最佳向量呢?我们首先发现,能够使投影后的两类样本中心点尽量分离的向量是好的向量,定量表示就是:
$$J(w)=|\tilde\mu_1-\tilde\mu_2|=|w^T(\mu_1-\mu_2)|$$
$J(w)$越大越好
但是只要考虑上面的显然不行,看下图: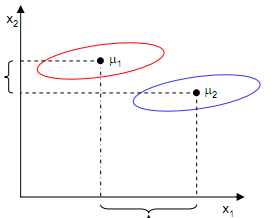
样本点均匀分布在椭圆里,投影到横轴$x_1$上时能够获得更大的中心点间距$J(w)$,但是由于有重叠,投影到$x_1$不能分离样本点。投影到纵轴$x_2$上,虽然$J(w)$较小,但是能够分离样本点。因此我们还需要考虑样本点之间的方差,方差越大,样本点越难以分离。
很当然的,我们使用散列值来度量投影后的分散程度:
$$\tilde s_i^2=\displaystyle\sum_{x\in\omega_i}(w^Tx-\tilde\mu_i)^2$$
我们想要投影后的样本点的样子是:不同类别的样本点越分开越好,同类的越聚集越好,也就是均值差越大越好,散列值越小越好。那么,最终的度量公式就是:
$$J(w)=\dfrac{|\tilde\mu_1-\tilde\mu_2|^2}{\tilde s_1^2+\tilde s_2^2}$$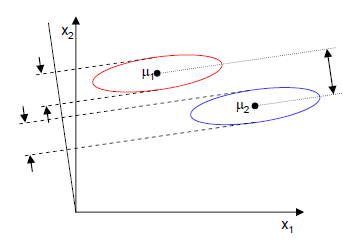
那么,我们只需要寻找使得$J(w)$最大的$w$即可。
先把散列值公式展开得到:
$$
\begin{array} {l l l}
\tilde s_i^2 & = & \displaystyle\sum_{x\in\omega_i}(w^Tx-\tilde\mu_i)^2 \\\
& = & \displaystyle\sum_{x\in\omega_i}(w^Tx-w^T\mu_i)^2 \\\
& = & \displaystyle\sum_{x\in\omega_i}w^T(x-\mu_i)(x-\mu_i)^Tw
\end{array}
$$
我们定义上式中间的部分$S_i=\displaystyle\sum_{x\in\omega_i}(x-\mu_i)(x-\mu_i)^T$
这个矩阵就是没除样本数的协方差矩阵,被称为散列矩阵(scatter matrix)。
我们继续定义
$$S_w=S_1+S_2$$
$S_w$被称为Within-class scatter matrix。
回到之前的公式,用新定义的符号代替原式子得
$$\tilde s_i^2=w^TS_iw$$
$$\tilde s_1^2+\tilde s_2^2=w^TS_ww$$
然后,展开分子
$$
\begin{array} {l l l}
(\tilde\mu_1-\tilde\mu_2)^2 & = & (w^T\mu_1-w^T\mu_2)^2 \\\
& = & w^T(\mu_1-\mu_2)(\mu_1-\mu_2)^Tw \\\
& = & w^TS_bw
\end{array}
$$
$S_b$被称为Between-class scatter matrix,是两个向量的外积,虽然是个矩阵,但是秩为1。
那么$J(w)$最终可以表示为
$$J(w)=\dfrac{w^TS_bw}{w^TS_ww}$$
在求导之前,我们需要对分母进行归一化,因为不做归一化的话,$w$扩大任何倍,都是成立的。为了确定某一个$w$值,我们人为定义$||w^TS_ww||=1$。那么,使用拉格朗日乘子法之后,得到:
$$
\begin{array} {l l l}
c(w) & = & w^TS_bw-\lambda(w^TS_ww-1) \\\
\Rightarrow \dfrac{dc(w)}{dw} & = & 2S_bw - 2\lambda S_ww = 0 \\\
\Rightarrow S_bw & = & \lambda S_ww
\end{array}
$$
其中用到了矩阵微积分,求导时可以简单的把$w^TS_ww$当成$S_ww^2$看待。
如果$S_w$可逆的话,那么将求导的结果两边同时乘以$S_w^{-1}$得到:
$$S_w^{-1}S_bw=\lambda w$$
那么$w$就是矩阵$S_w^{-1}S_b$的特征向量。
这个公式就是Fisher linear discrimination
我们再观察一下,发现:
$$
\begin{array} {l l l}
S_bw & = & (\mu_1-\mu_2)(\mu_1-\mu_2)^Tw \\\
& = & \lambda_w(\mu_1-\mu_2)
\end{array}
$$
代入最后的特征值公式得到
$$S_w^{-1}S_bw=\lambda_w\times S_w^{-1}(\mu_1-\mu_2)=\lambda w$$
由于对$w$扩大缩小多少倍都不会影响结果,因此可以约去两边的未知常数$\lambda$和$\lambda_w$,得到:
$$w=S_w^{-1}(\mu_1-\mu_2)$$
因此,我们只需要求出原始样本的均值和方差就可以求出最佳向量$w$,这就是Fisher于1936年提出的线性判别分析。
3、多类情况
前面是针对只有两个类别的情况,假设类别变成了多个,要怎么改变才能保证投影后不同类别能够分离呢?
我们之前讨论的是如何将$d$维降到$1$维,现在类别多了,$1$维可能已经不能满足要求了。假设我们有$C$个类别,需要$K$维向量(也可以叫基向量)来做投影,即将原来的$d$维数据降维到$K$维。
将这$K$维向量表示为$W=\begin{bmatrix} w_1 & w_2 & \dots & w_K \end{bmatrix}$。
我们将样本点在这$K$维向量投影后的结果表示为$W^Tx_i$。
为了像上一节一样定量度量$J(W)$,我们打算仍然从类间散列度和类内散列度来考虑。
当样本是二维的时候,我们从几何意义上考虑: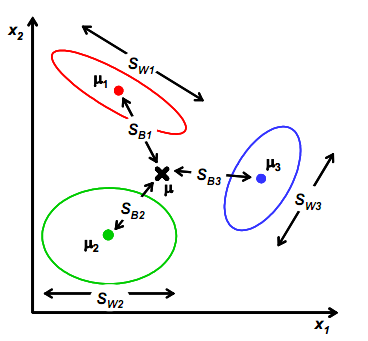
其中$\mu_i$和$S_w$与上节的意义一样,$S_{w1}$是类别1里面的样本点相对于该类点中心$\mu_i$的散列程度。$S_{b1}$变成类别1中心点相对于样本中心点$\mu$的协方差矩阵,即类1相对于$\mu$的散列程度。
$$S_w=\displaystyle\sum_{i=1}^CS_{wi}$$
$S_{wi}$的计算公式不变,仍然类似于类内部样本点的协方差矩阵。
$$S_{wi}=\displaystyle\sum_{x\in \omega_i}(x-\mu_i)(x-\mu_i)^T$$
$S_b$需要改变,原来度量的是两个均值点的散列情况,现在度量的是每类均值点相对于样本中心的散列情况。类似于将$\mu_i$看作样本点、$\mu$是均值的协方差矩阵。如果某类里面的样本点较多,那么其权重稍大,权重用$\dfrac{N_i}{N}$表示,但是由于$J(W)$对倍数不敏感,因此使用$N_i$。
$$S_b=\displaystyle\sum_{i=1}^CN_i(\mu_i-\mu)(\mu_i-\mu)^T$$
其中$\mu=\dfrac{1}{N}\displaystyle\sum_{\forall x}x=\frac{1}{N}\displaystyle\sum_{i=1}^CN_i\mu_i$是所有样本的均值。
上面讨论的都是在投影前的公式变化,但真正的$J(W)$的分子分母都是在投影后计算的。下面我们看样本点投影后的公式变化:
第$i$个样本点在某基向量上投影后的均值计算公式:
$$\tilde\mu_i=\frac{1}{N_i}\displaystyle\sum_{x\in\omega_i}W^Tx=W^T\frac{1}{N_i}\displaystyle\sum_{x\in\omega_i}x=W^T\mu_i$$
$$\tilde\mu=\frac{1}{N}\displaystyle\sum_{\forall x}W^Tx=W^T\frac{1}{N}\displaystyle\sum_{\forall x}x=W^T\mu$$
下面是在某基向量上投影后的$S_w$和$S_b$:
$$\begin{array} {l l l}
\tilde{S_w} & = & \displaystyle\sum_{i=1}^C\displaystyle\sum_{x\in\omega_i}(W^Tx-\tilde\mu_i)(W^Tx-\tilde\mu_i)^T \\\
& = & \displaystyle\sum_{i=1}^C\displaystyle\sum_{x\in\omega_i}W^T(x-\mu_i)(x-\mu_i)^TW \\\
& = & W^T\left(\displaystyle\sum_{i=1}^C\displaystyle\sum_{x\in\omega_i}(x-\mu_i)(x-\mu_i)^T\right)W \\\
& = & W^TS_wW
\end{array}
$$
$$
\begin{array} {l l l}
\tilde{S_b} & = & \displaystyle\sum_{i=1}^C(\tilde\mu_i-\tilde\mu)(\tilde\mu_i-\tilde\mu)^T \\\
& = & \displaystyle\sum_{i=1}^C(W^T\mu_i-W^T\mu)(W^T\mu_i-W^T\mu)^T \\\
& = & W^T\left(\displaystyle\sum_{i=1}^C(\mu_i-\mu)(\mu_i-\mu)^T\right)W \\\
& = & W^TS_bW
\end{array}
$$
回想我们上节的公式$J(W)$,分子是两类中心距,分母是每个类自己的散列度。现在投影方向是多维了,分子需要做出一些变化,我们不是求两两样本中心距之和(这个对描述类别间的分散程度没有任何用处),而是求每类中心相对于全样本中心的散列度之和。
因此,最后的$J(W)$的形式是
$$J(W)=\dfrac{|\tilde{S_b}|}{|\tilde{S_w}|}=\dfrac{|W^TS_bW|}{|W^TS_wW|}$$
整个问题又回归到求$J(W)$的最大值了,我们固定分母为1,然后求导,得到最后结果(这里不要以为形式差不多所以结果一定和上节一样,虽然确实是一样的,但是这里$w$从一个列向量变成了一个矩阵$W$。我们可以用拆分的思想来理解,如果矩阵的一个列向量满足某个等式,那么把这个矩阵拆成若干个列向量仍然满足这个等式,我们把最后的等式相加,重新将列向量组成矩阵,很显然是合理的):
$$S_bw_i=\lambda_i S_ww_i$$
$${S_w}^{-1}S_bw_i=\lambda_i w_i$$
与上节得出的结论一样!
这里求出来的特征值与对应的特征向量有$d$组,怎么取舍呢?
我们将得到的结论代入$J(w_i)$得到
$$J(w_i)=\dfrac{|w_i^T\lambda_iS_ww_i|}{|w_i^TS_ww_i|}=\lambda_i$$
要使得$J(w_i)$值最大,那么就取对应特征值最大的$K$个特征向量即可。
注意
由于$S_b$中$(\mu_i-\mu)$秩为1,因此$S_b$的秩至多为$C$(矩阵的秩小于等于各个相加矩阵的秩的和)。由于知道了前$C-1$个$\mu_i$后,最后一个$\mu_i$可以由前面的$\mu_i$来线性表示,因此$S_b$的秩至多为$C-1$,证明如下:
$$
\begin{array} {l l l}
\displaystyle\sum_{i=1}^CN_i(\mu_i-\mu) & = & \displaystyle\sum_{i=1}^CN_i\mu_i-\left(\displaystyle\sum_{i=1}^CN_i\right)\mu \\\
& = & \displaystyle\sum_{i=1}^C\displaystyle\sum_{x\in\omega_i}x-\displaystyle\sum_{\forall x}x \\\
& = & 0
\end{array}
$$
由于$S_w^{-1}S_b$不一定可逆,因此得到的$K$个特征向量不一定正交,这也是与PCA不同的地方。
4、实例
将三维空间的球体样本点投影到二维平面上,$w_1$比$w_2$能够获得更好的分离效果。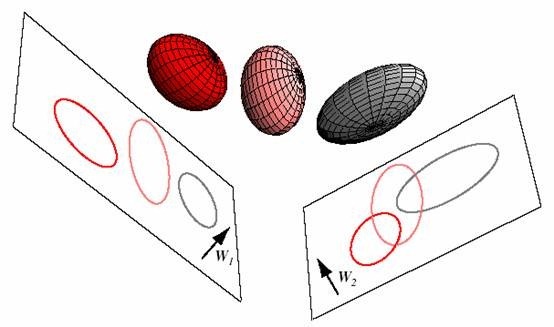
PCA与LDA的降维比较: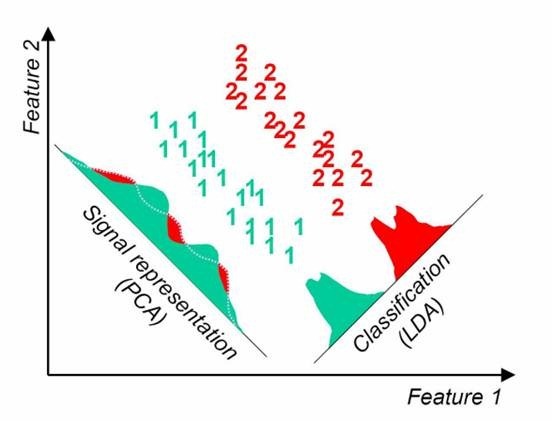
PCA选择样本点投影具有最大方差方向,LDA选择分类性能最好的方向。
5、使用LDA的一些限制
5-1、LDA至多可生成$C-1$维子空间
LDA降维后的维度区间是$[1,C-1]$,与原始特征数$d$无关,对于二值分类,最多投影到一维。
5-2、LDA不适合对非高斯分布样本进行降维
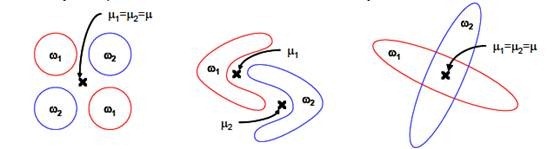
上图红色区域表示一类样本,蓝色区域表示一类样本,由于是两类,所以最多投影到一维上。不管在直线上怎么投影,都难以使红色点和蓝色点类内凝聚、类间分离。
5-3、LDA在样本分类信息依赖方差而不是均值时,效果不好
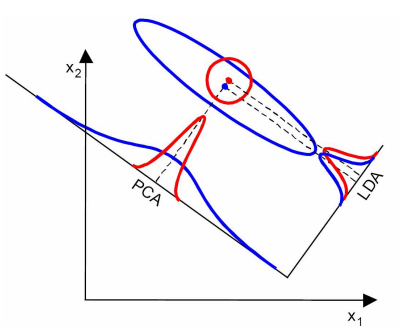
上图中,样本点依靠方差信息进行分类,而不是均值信息。LDA不能够进行有效分类,因为LDA过度依靠均值信息。
5-4、当$S_w$为奇异矩阵时,不能求出逆矩阵
先考虑什么情况下,$S_w$为奇异矩阵?
我们知道当样本数小于特征数的时候,求出的协方差矩阵不是满秩的,即协方差矩阵是不可逆的。因此,当特征数过多(大于样本数)的时候,我们就应该考虑怎么处理$S_w$不可逆的问题。
那么怎么解决呢?
一般在实现LDA算法时,都会对样本进行一次PCA算法的降维,消除样本的冗余,从而保证$S_w$是非奇异矩阵,当然即使$S_w$是奇异矩阵也是可解的,可以把$S_w$和$S_b$对角化。
5-5、LDA可能过度拟合数据
6、LDA的变种
6-1、非参数LDA
非参数LDA使用本地信息和$K$临近样本点来计算$S_b$,使得$S_b$是全秩的,这样我们可以抽取多于$C-1$个特征向量,而且投影后分离效果更好。
6-2、正交LDA
先找到最佳的特征向量,然后找到与这个特征向量正交且最大化Fisher条件的向量。这种方法也能摆脱$C-1$的限制。
6-3、一般化LDA
引入了贝叶斯风险等理论。
6-4、核函数LDA
将特征$x\rightarrow\Phi(x)$,使用核函数来计算。
7、一些问题
上面在多值分类中使用的
$$S_b=\displaystyle\sum_{i=1}^CN_i(\mu_i-\mu)(\mu_i-\mu)^T$$
是带权重的各类样本中心到全样本中心的散列矩阵。如果$C=2$(也就是二值分类)套用这个公式,不能够得出在二值分类中使用的$S_b$。
$$S_b=(\mu_1-\mu_2)(\mu_1-\mu_2)^T$$
因此二值分类和多值分类求得的$S_b$会不同,而$S_w$意义是一致的。
对于二值分类问题,令人惊奇的是最小二乘法和Fisher线性判别分析是一致的。
下面我们证明这个结论:
回想线性回归,给定$N$个$d$维特征的训练样本$X=\begin{bmatrix} x^{(1)} & x^{(2)} & \dots & x^{(N)}\end{bmatrix}$,每个$x^{(i)}$对应一个类标签$y^{(i)}$。我们之前令$y=0$表示一类、$y=1$表示另一类,现在我们为了证明最小二乘法和LDA的关系,我们需要做出一些改变(为了计算方便):
$$
\begin{cases}
y=\dfrac{N}{N_1}\text{,样例属于有$N_1$个元素的类$C_1$} \\\
y=-\dfrac{N}{N_2}\text{,样例属于有$N_2$个元素的类$C_2$}
\end{cases}
$$
就是将值$0/1$做了替换
我们列出最小二乘法公式:
$$E=\dfrac{1}{2}\displaystyle\sum_{i=1}^N(\theta^Tx^{(i)}+\theta_0-y^{(i)})^2$$
$\theta$和$\theta_0$是参数。
将上式对$\theta_0$求导得
$$
\begin{array} {l l l}
\displaystyle\sum_{i=1}^N(\theta^Tx^{(i)}+\theta_0-y^{(i)}) & = & 0 \\\
\theta^TN\mu+N\theta_0-\displaystyle\sum_{i=1}^Ny^{(i)} & = & 0 \\\
\theta^TN\mu+N\theta_0-\left(N_1\dfrac{N}{N_1}-N_2\dfrac{N}{N_2}\right) & = & 0 \\\
\theta_0 & = & -\theta^T\mu
\end{array}
$$
而且$\mu=\dfrac{1}{N}\displaystyle\sum_{i=1}^Nx^{(i)}=\frac{1}{N}(N_1\mu_1+N_2\mu_2)$
然后对$\theta$求导得到
$$\displaystyle\sum_{i=1}^N\left(\theta^Tx^{(i)}+\theta_0-y^{(i)}\right)x^{(i)}=0$$
我们不妨将$x^{(i)}$转置方便计算而且不影响整个过程,得到:
$$
\begin{array} {l l l}
\displaystyle\sum_{i=1}^N\left(\theta^Tx^{(i)}+\theta_0-y^{(i)}\right)(x^{(i)})^T & = & 0 \\\
\displaystyle\sum_{i=1}^N\theta^Tx^{(i)}(x^{(i)})^T+\displaystyle\sum_{i=1}^N\theta_0(x^{(i)})^T-\displaystyle\sum_{i=1}^Ny^{(i)}(x^{(i)})^T & = & 0 \\\
\displaystyle\sum_{i=1}^N\theta^Tx^{(i)}(x^{(i)})^T-\displaystyle\sum_{i=1}^N\theta^T\mu (x^{(i)})^T-\left(\dfrac{N}{N_1}N_1\mu_1^T-\dfrac{N}{N_2}N_2\mu_2^T\right) & = & 0 \\\
\theta^T\left(\displaystyle\sum_{i=1}^N(x^{(i)}-\mu)(x^{(i)})^T\right) & = & N(\mu_1^T-\mu_2^T) \\\
\theta^T\left(S_w+\displaystyle\sum_{i=1}^N(x^{(i)}-\mu)(x^{(i)})^T-\displaystyle\sum_{x^{(i)}\in\omega_1}(x^{(i)}-\mu_1)(x^{(i)}-\mu_1)^T-\displaystyle\sum_{x^{(i)}\in\omega_2}(x^{(i)}-\mu_2)(x^{(i)}-\mu_2)^T\right) & = & N(\mu_1^T-\mu_2^T) \\\
\theta^T\left(S_w+\displaystyle\sum_{x^{(i)}\in\omega_1}\left(x^{(i)}(x^{(i)})^T-\mu(x^{(i)})^T-x^{(i)}(x^{(i)})^T+\mu_1(x^{(i)})^T+x^{(i)}\mu_1^T-\mu_1\mu_1^T\right) \\\
+\displaystyle\sum_{x^{(i)}\in\omega_2}\left(x^{(i)}(x^{(i)})^T-\mu(x^{(i)})^T-x^{(i)}(x^{(i)})^T+\mu_2(x^{(i)})^T+x^{(i)}\mu_2^T-\mu_2\mu_2^T\right)\right) & = & N(\mu_1^T-\mu_2^T) \\\
\theta^T\left(S_w+\displaystyle\sum_{x^{(i)}\in\omega_1}\left(\dfrac{N_2}{N}(\mu_1-\mu_2)(x^{(i)})^T+x^{(i)}\mu_1^T-\mu_1\mu_1^T\right)+\displaystyle\sum_{x^{(i)}\in\omega_2}\left(\dfrac{N_1}{N}(\mu_2-\mu_1)(x^{(i)})^T+x^{(i)}\mu_2^T-\mu_2\mu_2^T\right)\right) & = & N(\mu_1^T-\mu_2^T) \\\
\theta^T\left(S_w+\dfrac{N_1N_2}{N}(\mu_1-\mu_2)\mu_1^T+N_1\mu_1\mu_1^T-N_1\mu_1\mu_1^T+\dfrac{N_1N_2}{N}(\mu_2-\mu_1)\mu_2^T+N_2\mu_2\mu_2^T-N_2\mu_2\mu_2^T\right) & = & N(\mu_1^T-\mu_2^T) \\\
\theta^T\left(S_w+\dfrac{N_1N_2}{N}(\mu_1-\mu_2)(\mu_1-\mu_2)^T\right) & = & N(\mu_1^T-\mu_2^T) \\\
\theta^T\left(S_w+\dfrac{N_1N_2}{N}S_b\right) & = & N(\mu_1^T-\mu_2^T) \\\
\end{array}
$$
然后将等式两边再进行转置操作,结果不会改变:
$$(S_w+\dfrac{N_1N_2}{N}S_b)\theta=N(\mu_1-\mu_2)$$
由于$S_b\theta=\lambda_w\times(\mu_1-\mu_2)$
最后得到的结果仍然是
$$\theta=S_w^{-1}(\mu_1-\mu_2)$$
这个过程从几何意义上去理解也就是变形后的线性回归(将类标签重新定义),线性回归后的直线方向就是二值分类中LDA求得的直线方向$w$。
好了,我们从改变后的$y$的定义可以看出$y>0$属于类$C_1$,$y< 0$属于类$C_2$。因此我们可以选取$y_0=0$作为阈值,即如果$h_\theta(x)=\theta^Tx+\theta_0>0$,就是类$C_1$,否则是类$C_2$。
8、算法实现
8-1、LDA算法
总结一下LDA的算法步骤:
设有$m$条$n$维数据
1)将原始数据按行组成$m$行$n$列矩阵$X$
2)找出所有不同的类别,求出类别数$C$
3)求出所有样本点均值$\mu$,每个类别的样本点均值$\mu_i$和样本数$num$
4)利用$S_w=\displaystyle\sum_{i=1}^C\displaystyle\sum_{x\in\omega_i}(x-\mu_i)(x-\mu_i)^T$公式求出类内散列矩阵$S_w$
5)如果$C$=2,利用$S_w^{-1}(\mu_1-\mu_2)$公式求出结果,程序结束
6)如果$C$>2,利用$S_b=\displaystyle\sum_{i=1}^CN_i(\mu_i-\mu)(\mu_i-\mu)^T$公式求出类间散列矩阵$S_b$
7)求出$S_w^{-1}S_b$的特征值与对应的特征向量
8)将特征向量按对应特征值大小从上到下按行排列成矩阵,取前$C-1$行组成矩阵$P$
9)$Y=PX$即为降维到$C-1$维后的数据
8-2、关键代码
|
|
完整代码请点击shengtao96-github-lda
9、总结
线性判别分析的基本思想是将高维的模式样本投影到最佳鉴别矢量空间,以达到抽取分类信息和压缩特征空间维数的效果,投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离,即模式在该空间中有最佳的可分离性。因此,它是一种有效的特征抽取方法。