贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。这篇文章先介绍一下贝叶斯分类的基础——贝叶斯定理,然后讨论贝叶斯分类中最简单的一种:朴素贝叶斯分类。
这篇文章的目的是记录我学习朴素贝叶斯过程的心得体会,介绍一下贝叶斯定理,文章有问题的地方欢迎指正。
1、概率基础
在开始介绍贝叶斯之前,先简单介绍下概率的基础知识。概率是某一结果出现的可能性的数值表示。例如,抛一枚均质硬币,正面朝上的可能性多大?$0.5$!概率值是一个$0$~$1$之间的浮点数,用来定量地衡量一个事件发生的可能性的大小。概率值越接近$1$,事件发生的可能性越大;概率值越接近$0$,事件越不可能发生。我们日常生活中听到最多的概率是天气预报的降水概率。概率的一种表示方法叫维恩图。下面通过维恩图来说明贝叶斯公式中常见的几个概率: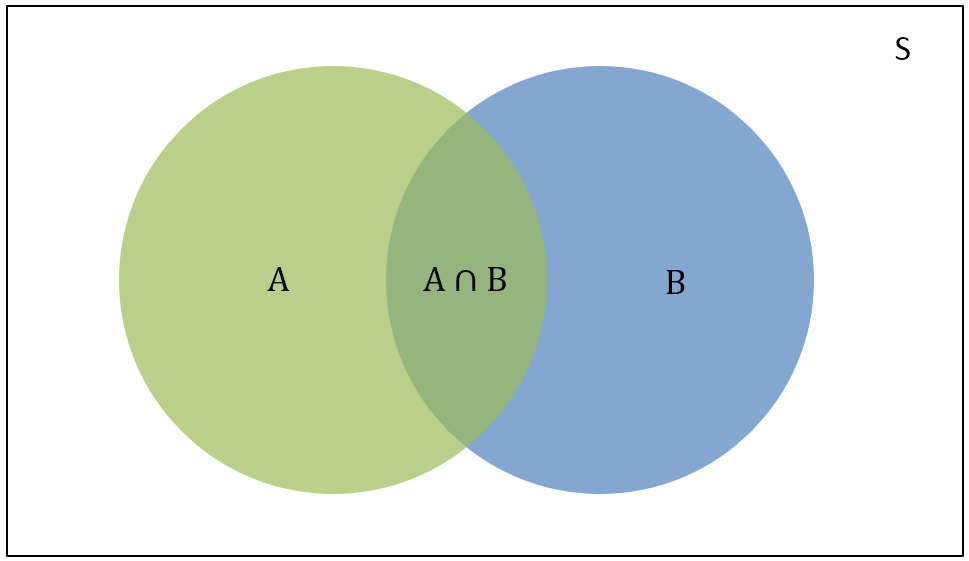
在维恩图中:
$S$:是样本空间,是所有可能事件的总和。
$P(A)$:是样本空间$S$中事件$A$发生的概率,维恩图中绿色的部分。
$P(B)$:是样本空间$S$中事件$B$发生的概率,维恩图中蓝色的部分。
$P(A\cap B)$:是样本空间$S$中事件$A$和事件$B$同时发生的概率,也就是$A$和$B$相交的部分。
$P(A|B)$:是条件概率,是事件$B$已经发生时事件$A$发生的概率。
对于条件概率,还有一种更清晰的表示方法叫概率树。下面的概率树表示了条件概率$P(A|B)$。与维恩图中的$P(A\cap B)$相比,可以发现两者明显的区别。$P(A\cap B)$是事件$A$和事件$B$同时发生的情况,因此是两者相交区域的概率。而事件概率$P(A|B)$是事件$B$发生时事件$A$发生的概率。这里有一个先决条件就是$P(B)$要首先发生。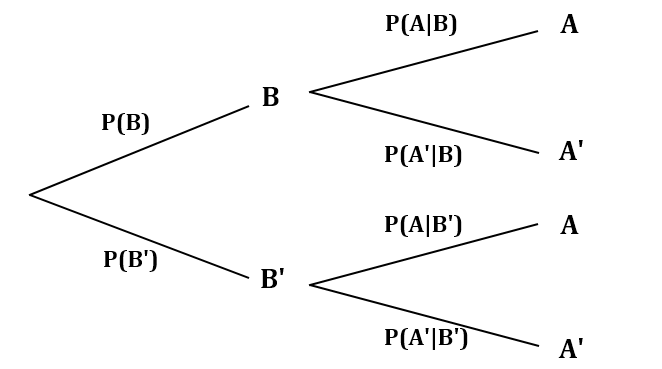
因为条件概率$P(A|B)$是在事件$B$已经发生的情况下,事件$A$发生的概率,所以$P(A|B)$可以表示为事件$A$与$B$的交集与事件$B$的比值。
$$P(A|B)=\dfrac{P(A\cap B)}{P(B)}$$
该公式还可以转换一下形式,以便我们下面进行贝叶斯公式计算时使用。
$$P(A\cap B)=P(A|B)\times P(B)$$
2、贝叶斯公式
贝叶斯公式通过已知的$P(A|B)$,$P(A)$和$P(B)$三个概率计算$P(B|A)$发生的概率。通过前面的概率树及$P(A|B)$的概率可知,$P(B|A)$的概率是在事件$A$发生的前提下事件$B$发生的概率,因此$P(B|A)$可以表示为事件$B$与事件$A$的交集与事件$B$的比值。
$$P(B|A)=\dfrac{P(B\cap A)}{P(A)}$$
该公式同样可以转化为以下形式:
$$P(B\cap A)=P(B|A)\times P(A)$$
根据上一节得到的结论,很显然的得贝叶斯公式:
$$P(B|A)=\dfrac{P(A|B)P(B)}{P(A)}$$
3、贝叶斯推断
在贝叶斯公式中,每一种概率都有一个特定的名字:
$P(B)$是“先验概率”(Prior Probability)
$P(A)$是“先验概率”(Prior Probability),也叫做标准化常量(Normalized constant)
$P(A|B)$是已知$B$发生后$A$的条件概率,叫做似然函数(likelihood)
$P(B|A)$是已知$A$发生后$B$的条件概率,是我们要求的值,叫做后验概率
$P(A|B)/P(A)$是调整因子,也被称作标准似然度(Stand
ardised likelihood)
$$P(B|A)=P(B)\times\dfrac{P(A|B)}{P(A)}$$
贝叶斯推断中有几个关键的概念需要说明下:
第一个是先验概率,先验概率是指我们主观通过事件发生次数对概率的估计。
第二个是似然函数,似然函数是对某事件发生可能性的判断,与条件概率正好相反。通过事件已经发生的情况推算事件可能性的概率。
对比似然函数与概率
概率:给定某一参数值,求某一结果的可能性。
例如,抛一枚均质硬币,抛10次,6次正面向上的可能性是多大?
似然函数:给定某一结果,求某一参数值的可能性。
例如,抛一枚硬币,抛10次,结果6次正面向上,其是均质的可能性多大?
第三个是调整因子,调整因子是似然函数与先验概率的比值,这个比值相当于一个权值,用来调整后验概率的值,使后验概率更接近真实概率。
因此,贝叶斯推断可以理解为通过先验概率和调整因子来获得后验概率。其中调整因子是根据事件已经发生的情况下推断事件可能发生的概率(通过硬币正面出现的次数来推断硬币均匀的可能性),并与已经发生的先验概率(硬币正面出现的概率)的比值。通过这个比值调整先验概率来获得后验概率。
$$后验概率=先验概率\times调整因子$$
4、朴素思想
朴素贝叶斯的思想基础是这样的:对于给出的待分类样本,求解在此样本特征条件下属于各个类别的概率,哪个最大,就认为此待分类样本属于哪个类别。
通俗来说,就好比这么个道理,你在街上看到一个黑人,我问你你猜这哥们哪来的,你十有八九猜非洲。为什么?因为黑人中非洲人的比率最高,当然人家也可能是美洲人或亚洲人,但在没有其它可用信息下,我们会选择条件概率最大的类别,这就是朴素贝叶斯的思想基础。
在朴素贝叶斯应用的问题中,每个样本$x$可由特征值的合取来描述,而分类器$f(x)$从某有限集合$\omega$中取值。分类器被提供一个已经分好类别的训练集,以及待分类样本$< a_1,a_2,\dots,a_n >$,然后要求预测待分类样本的类别。
贝叶斯分类器的任务就是在给定样本的特征值$< a_1,a_2,\dots,a_n >$下,得到最可能的类别$\omega_{MAP}$。
$$\omega_{MAP}=\arg_{\omega_i\in\omega}\max P(\omega_i|a_1,a_2,\dots,a_n)$$
可以使用贝叶斯公式将此表达式重写为:
$$\omega_{MAP}=\arg_{\omega_i\in\omega}\max\dfrac{P(a_1,a_2,\dots,a_n|\omega_i)P(\omega_i)}{P(a_1,a_2,\dots,a_n)}=\arg_{\omega_i\in\omega}\max P(a_1,a_2,\dots,a_n|\omega_i)P(\omega_i)$$
那么我们需要做的就是估计出,基于训练数据的上式的每个类别项的值,比较大小。估计$P(\omega_i)$很容易,只要计算每个类别$\omega_i$出现在训练数据中的频率即可。
然而用同样的方法估计$P(a_1,a_2,\dots,a_n|\omega_i)$项是不可能的。问题在于这些项的数量等于可能样本的数量乘以可能类别的数量。因此,为获得合理估计,样本空间中的每个样本必须出现足够多次。
为了解决这个问题,朴素贝叶斯分类器基于一个简单的假定:在给定类别时,特征值之间互相条件独立。
换言之,该假定使得在给定样本类别的情况下,$< a_1,a_2,\dots,a_n >$的概率是对每个单独特征的概率的乘积:
$$\omega_{NB}=\arg_{\omega_i\in\omega}\max P(\omega_i)\displaystyle\prod_j^n P(a_j|\omega_i)$$
其中$\omega_{NB}$表示朴素贝叶斯分类器输出的类别。
注意在朴素贝叶斯分类器中,须从训练数据中估计不同$P(a_j|\omega_i)$的数量只是不同的特征值数量乘以不同的类别值数量——这比要估计$P(a_1,a_2,\dots,a_n|\omega_i)$项所需的工程要小得多。
5、朴素贝叶斯分类
概括地说,朴素贝叶斯需要估计不同的$P(\omega_i)$和$P(a_j|\omega_i)$项,基于它们在训练数据上的频率。这些估计值对应了待分类样本的假设,然后该假设使用上面式子中的规则来分类新样本。只要所需的条件独立性能够被满足,朴素贝叶斯分类$\omega_{Nb}$等于$\omega_{MAP}$。
朴素贝叶斯分类的正式定义如下:
1、设$x=< a_1,a_2,\dots,a_n >$为一个待分类样本,而每个$a_j$为$x$的一个特征属性
2、有类别集合$C=\{y_1,y_2,\dots,y_m\}$。
3、估计$P(y_1|x),P(x_2|x),\dots,P(y_m|x)$。
4、如果$P(y_k|x)=\max\{P(y_1|x),P(y_2|x),\dots,P(y_m|x)\}$,则$x\in y_k$。
那么现在的关键就是如何估计第3步中的各个条件概率。我们可以这么做:
1、收集训练样本数据,形成训练集。
2、统计得到在各个类别下各个特征属性的条件概率,即$P(a_1|y_1),P(a_2|y_1),\dots,P(a_n|y_1);P(a_1|y_2),P(a_2|y_2),\dots,P(a_n|y_2);\dots;P(a_1|y_m),P(a_2|y_m),\dots,P(a_n|y_m)$。
3、假设两两特征之间是条件独立的,则根据贝叶斯公式有:
$$P(y_i|x)\propto P(x|y_i)P(y_i)=P(a_1|y_i)P(a_2|y_i)\dots P(a_m|y_i)P(y_i)=P(y_i)\displaystyle\prod_{j=1}^mP(a_j|y_i)$$
6、特征值连续以及Laplace Smoothing
由上文看出,计算各个类别的条件概率$P(a_j|y_i)$是朴素贝叶斯分类的关键性步骤,当特征属性为离散值时,只要很方便的统计训练集中各个类别中出现的频率即可估计$P(a_j|y_i)$,下面谈谈特征属性是连续值的情况。
当特征属性为连续值时,通常假定其服从高斯分布(正态分布),即:
$$g(x,\eta,\sigma)=\dfrac{1}{\sqrt{2\pi}\sigma}e^{-\dfrac{(x-\eta)^2}{2\sigma^2}}$$
$$P(a_j|y_i)=g(a_j,\eta_{y_i},\sigma_{y_i})$$
因此只要计算出训练集中各个类别中此特征项划分的各均值和标准差,代入上式即可得到需要的估计值。
另一个需要讨论的是当$P(a_j|y_i)=0$怎么办。当某个类别下某个特征值没有出现过,会直接导致这种类别的可能性为$0$,这会使分类器质量大大降低。为了解决这个问题,我们使用Laplace Smoothing,做法很简单,对所有$P(a_j|y_i)=0$的估计,分子加+1,分母加上不同的特征值个数。这样只是将数值减小,不会对分类结果产生影响,同时解决了频率为$0$的问题。
$$P(a_{jk}|\omega_i)=\dfrac{|a_j=a_{jk}\land\omega=\omega_i|+1}{|\omega=\omega_i|+|a_j|}$$
$P(a_{jk}|\omega_i)$表示样本属于类别$\omega_i$的情况下,第$j$个特征值等于$k$的概率大小。
$|a_j=a_{jk}\land\omega=\omega_i|$表示训练集中类别为$\omega_i$且第$j$个特征值等于$k$的样本个数。
$|\omega=\omega_i|$表示训练集中类别为$\omega_i$的样本个数。
$|a_j|$表示训练集中第$j$个特征出现的不同值的个数。
7、算法实现
7-1、NB算法
总结一下NB的算法步骤
1、建立分类器的算法
1)对每个特征量,根据训练集中的所有样本在这个特征量上的取值$dataMat$,构建训练集在这个特征量上的可能取值的集合$dataCat$
2)根据训练集的所有类别$labelMat$,构建类别可能取值的集合$labelCat$
3)对每个类别,根据训练集的所有类别$labelMat$,构建每个类别在训练集中的样本个数$labelSum$
4)对每个特征量,对每个类别,对每个特征量的可能取值,根据训练集中的样本特征$dataMat$以及类别$labelMat$,构建这个特征取这个可能取值而且在样本属于这个类别的样本个数$dataSum$
5)以$dataCat$、$dataSum$、$labelCat$和$labelSum$作为朴素贝叶斯的分类器进行分类
2、进行分类的算法
1)得到测试样本$testEntry$与分类器($dataCat$、$dataSum$、$labelCat$和$labelSum$)
2)对每个类别,计算在测试样本$testEntry$的情况下,样本属于该类别的概率$pClass$
3)对每个特征量,计算在该类别下该特征量取值与$testEntry$相同的概率,同时将结果累乘$pClass$
4)将累乘结果$pClass$再乘以,该类别个数在所有训练集样本中的比率
5)将测试样本属于每个类别的概率$pClass$求出来,进行比较,分类给概率最大的类别
7-2、关键代码
|
|
完整代码请点击shengtao96-hithub-nb